(本小题满分12分)已知数列{an}的前n项和为Sn, 且满足条件：4S n =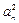
+ 4n – 1 , nÎN*.
(1) 证明：(a n– 2)2 –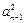
="0" （n ³ 2）;(2) 满足条件的数列不惟一，试至少求出数列{an}的的3个不同的通项公式 .
相关试题
的焦点坐标为
，过
的直线交抛物线
于
两点，直线
分别与直线
：
相交于
两点．
中,底面
是边长为
的正方形,侧面
底面
,设
、
分别为
、
的中点．
//平面
．
的首项
，公差
．且
分别是等比数列
的
.
与
的通项公式；
对任意自然数
均有
成立，求
的值.
．
的最大值．
，
.
的单调性；
，使得
成立，求满足上述条件的最大整数
；
，都有
成立，求实数
的取值范围.推荐套卷
(本小题满分12分)已知数列{an}的前n项和为Sn, 且满足条件：4S n =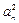+ 4n – 1 , nÎN*.
(1) 证明：(a n– 2)2 –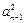="0" （n ³ 2）;(2) 满足条件的数列不惟一，试至少求出数列{an}的的3个不同的通项公式 .
粤公网安备 44130202000953号