(本小题满分14分)已知椭圆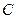 以
以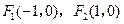 为焦点,且离心率
为焦点,且离心率 .
.
(Ⅰ)求椭圆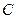 的方程;
的方程;
(Ⅱ)过 点斜率为
点斜率为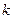 的直线
的直线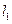 与椭圆
与椭圆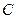 有两个不同交点
有两个不同交点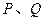 ,求
,求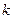 的范围。
的范围。
(Ⅲ)设椭圆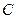 与
与 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为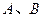 ,是否存在直线
,是否存在直线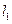 ,满足(Ⅱ)中的条件且使得向量
,满足(Ⅱ)中的条件且使得向量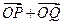 与
与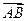 垂直?如果存在,写出
垂直?如果存在,写出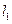 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。
推荐套卷
(本小题满分14分)已知椭圆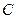 以
以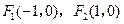 为焦点,且离心率
为焦点,且离心率 .
.
(Ⅰ)求椭圆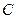 的方程;
的方程;
(Ⅱ)过 点斜率为
点斜率为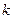 的直线
的直线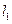 与椭圆
与椭圆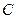 有两个不同交点
有两个不同交点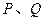 ,求
,求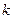 的范围。
的范围。
(Ⅲ)设椭圆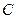 与
与 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为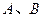 ,是否存在直线
,是否存在直线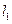 ,满足(Ⅱ)中的条件且使得向量
,满足(Ⅱ)中的条件且使得向量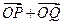 与
与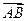 垂直?如果存在,写出
垂直?如果存在,写出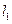 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。