已知抛物线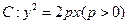
上任意一点到焦点F的距离比到
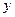轴的距离大1，（1）求抛物线C的方程；（2）若过焦点F的直线交抛物线于M，N两点，M在第一象限，且
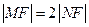，求直线MN的方程；（3）过点
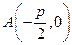的直线交抛物线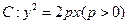于P、Q两点，设点P关于
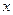轴的对称点为R，求证：直线RQ必过定点．
相关试题
，分别用“For”语句和“While”语句描述计算S这一问题的算法过程.
的值.要求画出程序框图，写出用基本语句编写的程序.
（单位：元）为托运费，ω为托运物品的重量（单位：千克），试写出一个计算费用推荐套卷
已知抛物线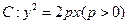上任意一点到焦点F的距离比到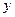轴的距离大1，（1）求抛物线C的方程；（2）若过焦点F的直线交抛物线于M，N两点，M在第一象限，且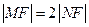，求直线MN的方程；（3）过点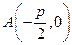的直线交抛物线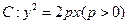于P、Q两点，设点P关于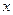轴的对称点为R，求证：直线RQ必过定点．
粤公网安备 44130202000953号