如图,在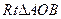 中,
中,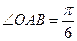 ,斜边
,斜边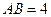 ,
,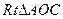 可通过
可通过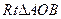 以直线AO为轴旋转得到,且二面角
以直线AO为轴旋转得到,且二面角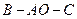 是直二面角,动点D在斜边AB上,(1)求证:平面
是直二面角,动点D在斜边AB上,(1)求证:平面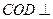 平面
平面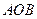 ;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面
;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面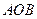 所成最大值角的正切值.
所成最大值角的正切值.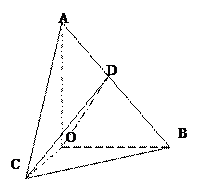
推荐套卷
如图,在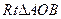 中,
中,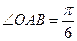 ,斜边
,斜边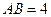 ,
,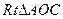 可通过
可通过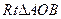 以直线AO为轴旋转得到,且二面角
以直线AO为轴旋转得到,且二面角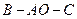 是直二面角,动点D在斜边AB上,(1)求证:平面
是直二面角,动点D在斜边AB上,(1)求证:平面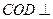 平面
平面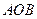 ;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面
;(2)当D为AB的中点时,求异面直线AO与CD所成角的正切值;(3)求CD与平面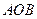 所成最大值角的正切值.
所成最大值角的正切值.