福建省厦门市高三5月适应性考试理科数学试卷
“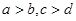 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知服从正态分布 的随机变量在区间
的随机变量在区间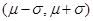 ,
,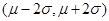 和
和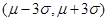 内取值的概率分别为68.3%,95.4%和99.7%.某校高一年级1000名学生的某次考试成绩服从正态分布
内取值的概率分别为68.3%,95.4%和99.7%.某校高一年级1000名学生的某次考试成绩服从正态分布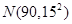 ,则此次成绩在(60,120)范围内的学生大约有( )
,则此次成绩在(60,120)范围内的学生大约有( )
| A.997人 | B.972人 | C.954人 | D.683人 |
甲、乙、丙、丁四个人排成一行,则乙、丙位于甲的同侧的排法种数是( )
| A.16 | B.12 | C.8 | D.6 |
数列 的前
的前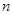 项和为
项和为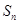 ,前
,前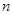 项积为
项积为 ,且
,且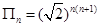 ,则
,则 等于( )
等于( )
|
A.31 B.62 C.124 D.126
在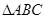 中,
中, 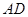 是
是 边上的高,给出下列结论:
边上的高,给出下列结论:
①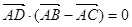 ; ②
; ②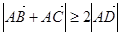 ; ③
; ③ ;
;
其中结论正确的个数是( )
A. |
B. |
C.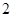 |
D.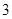 |
如图,棱长为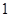 的正方体
的正方体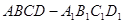 中,
中, 为线段
为线段 上的动点,则下列结论错误的是
上的动点,则下列结论错误的是
A.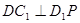 |
B.平面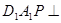 平面 平面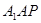 |
C.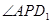 的最大值为 的最大值为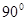 |
D.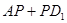 的最小值为 的最小值为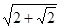 |
已知圆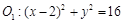 和圆
和圆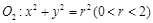 ,动圆M与圆
,动圆M与圆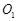 ,圆
,圆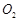 都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为
都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为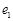 ,
,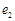 (
(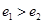 ),则
),则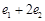 的最小值是( )
的最小值是( )
A.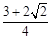 |
B.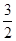 |
C.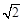 |
D.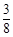 |
甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示.现从这 20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)的值是 .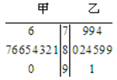
A、B两地相距1千米,B、C两地相距3千米,甲从A地出发,经过B前往C地,乙同时从B地出发,前往C地.甲、乙的速度关于时间的关系式分别为 和
和 (单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述:
(单位:千米/小时).甲、乙从起点到终点的过程中,给出下列描述:
①出发后1小时,甲还没追上乙 ② 出发后1小时,甲乙相距最远
③甲追上乙后,又被乙追上,乙先到达C地 ④甲追上乙后,先到达C地
其中正确的是 .(请填上所有描述正确的序号)
如图1,直角梯形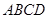 中,
中,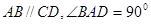 ,
,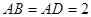 ,
,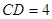 ,点
,点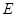 为线段
为线段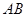 上异于
上异于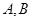 的点,且
的点,且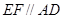 ,沿
,沿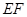 将面
将面 折起,使平面
折起,使平面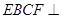 平面
平面 ,如图2.
,如图2.
(1)求证: 平面
平面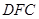 ;
;
(2)当三棱锥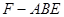 体积最大时,求平面
体积最大时,求平面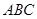 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.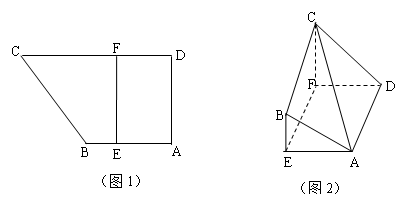
已知圆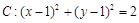 经过椭圆
经过椭圆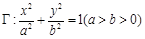 的右焦点
的右焦点 和上顶点
和上顶点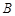 .
.
(1)求椭圆 的方程;
的方程;
(2)过原点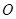 的射线
的射线 与椭圆
与椭圆 在第一象限的交点为
在第一象限的交点为 ,与圆
,与圆 的交点为
的交点为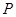 ,
,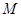 为
为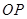 的中点,求
的中点,求 的最大值.
的最大值.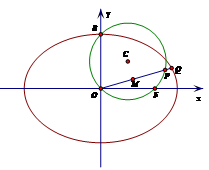
自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
| |
CD段 |
EF段 |
GH段 |
| 堵车概率 |
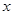 |
 |
 |
| 平均堵车时间 (单位:小时) |
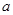 |
2 |
1 |
经调查发现,堵车概率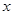 在
在 上变化,
上变化, 在
在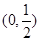 上变化.
上变化.
在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
| 堵车时间(单位:小时) |
频数 |
| [0,1] |
8 |
| (1, 2] |
6 |
| (2, 3] |
38 |
| (3, 4] |
24 |
| (4, 5] |
24 |
(1)求 段平均堵车时间
段平均堵车时间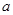 的值;
的值;
(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
已知函数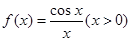 ,
,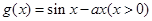 .
.
(1)函数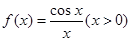 的零点从小到大排列,记为数列
的零点从小到大排列,记为数列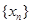 ,求
,求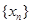 的前
的前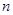 项和
项和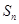 ;
;
(2)若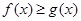 在
在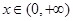 上恒成立,求实数
上恒成立,求实数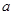 的取值范围;
的取值范围;
(3)设点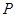 是函数
是函数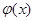 与
与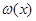 图象的交点,若直线
图象的交点,若直线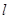 同时与函数
同时与函数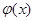 ,
,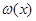 的图象相切于
的图象相切于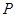 点,且
点,且
函数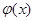 ,
,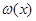 的图象位于直线
的图象位于直线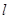 的两侧,则称直线
的两侧,则称直线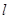 为函数
为函数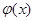 ,
,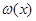 的分切线.
的分切线.
探究:是否存在实数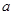 ,使得函数
,使得函数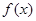 与
与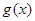 存在分切线?若存在,求出实数
存在分切线?若存在,求出实数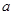 的值,并写出分切线方程;若不存在,请说明理由.
的值,并写出分切线方程;若不存在,请说明理由.
已知在矩阵M对应的变换作用下,点A(1,0)变为A′(1,0),点B(1,1)变为B′(2,1).
(1)求矩阵M;
(2)求 ,
,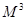 ,并猜测
,并猜测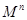 (只写结果,不必证明).
(只写结果,不必证明).
在平面直角坐标系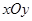 中,以
中,以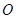 为极点,
为极点,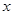 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线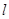 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,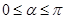 ).
).
(1)写出直线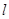 的直角坐标方程;
的直角坐标方程;
(2)求直线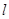 与曲线
与曲线 的交点的直角坐标.
的交点的直角坐标.
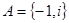 ,
,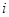 为虚数单位,则下列选项正确的是( )
为虚数单位,则下列选项正确的是( )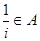
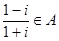
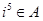
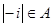
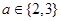 ,
,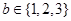 ,执行右边程序框图,则输出的结果共有( )
,执行右边程序框图,则输出的结果共有( )
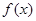 是周期为4的奇函数,当
是周期为4的奇函数,当 时,
时,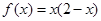 ,则
,则 等于 ( )
等于 ( )

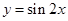 的图象向右平移3个单位后,得到函数
的图象向右平移3个单位后,得到函数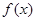 的图象,则函数
的图象,则函数 则满足
则满足 的实数
的实数 的取值范围是 .
的取值范围是 . 表示区域为
表示区域为 ,且圆
,且圆 在
在 ,则实数
,则实数 的值等于 .
的值等于 . .
. 的单调递增区间;
的单调递增区间; 是
是 的三个内角,且
的三个内角,且 ,
, ,又
,又 ,求
,求 边的长.
边的长. ,且
,且 ,
, 的最小值为
的最小值为 .
. 的不等式
的不等式 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号