山东潍坊市四县市七年级第二学期期末质量监测数学
(11·贺州)
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为2 000千克/亩、2 500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地收获两种生姜的年总产量为68 000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,
全部收购该基地生姜的年总收入最多?最多是多少元?
(11·贺州)
某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长(精确到0.1米);
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确
保安全 吗?
吗?
(参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.48,sin 58°12’≈0.85,tan 49°30’
≈1.17)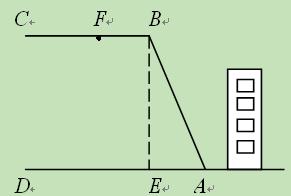
(11·贺州)
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线
交于点E.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
法);

(11·贺州).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴 与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
请直接写出满足条件的所有点P的坐标.
(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF
∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求
出S的最大值及此时E点的坐标;若不存在,请说明理由.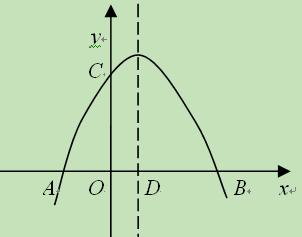
由方程组 可得出x与y的关系式是( )
可得出x与y的关系式是( )
| A.x+y=9 | B.x+y=3 |
| C.x+y=-3 | D.x+y=-9 |
在1,2,3,-4这四个数中,任选两个数的积作为k的值,使反比例函数 的图象在第二、四象限的概率是( )
的图象在第二、四象限的概率是( )
A. |
B. |
C. |
D. |
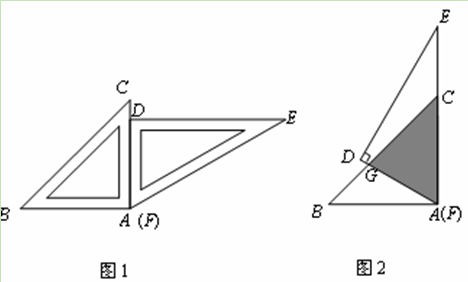
一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),
测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( )
| A.75cm2 | B. cm2 cm2 |
C.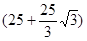 cm2 cm2 |
D.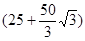 cm2 cm2 |
如图,矩形ABCD中,AB=4,以点B为圆心,BA为半径画弧交BC于点E,以点O为圆心的⊙O与弧 ,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为( )
,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为( )
| A.4 | B. |
C. |
D.5 |
根据右图中已填出的“√”和“×”的排列规律,把②、③、④还原为“√”或“×”且
符合右图的排列规律,下面“ ”中还原正确的是( )

某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结
束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 人.
如图,正方体的棱长为3,点M,N分别在CD,HE上, ,
, ,HC与NM的延长线交于点P,则tan∠NPH的值为 .
,HC与NM的延长线交于点P,则tan∠NPH的值为 .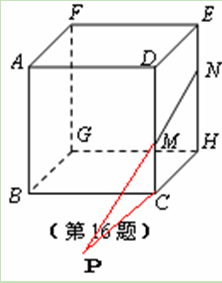
如图,正方形ABCD的边长为2,点E是BC边的中点,过点B作BG⊥AE,
垂足为G,延长BG交AC于点F,则CF= .
(8分)如图,直线AB,CD分别与直线AC相交于点A,C,与
直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
(8分)“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘音乐
教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并
按2:3:5的比 例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音
例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音
乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩
见下表:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 笔试成绩 |
 66 66 |
90 |
86 |
64 |
65 |
84 |
| 专业技能测试成绩 |
95 |
92 |
93 |
80 |
88 |
92 |
| 说课成绩 |
85 |
78 |
86 |
88 |
94 |
85 |
(1)笔试成绩的极差是多少?
(2)写出说课成绩的中位数、众数;
(3)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
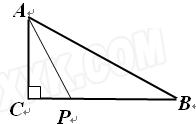
如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是
| A.2.5 | B.3 | C.4 | D.5 |
今年1季度,某市高新技术产业产值突破110亿元,同比增长59%.数据“110
亿”用科学记数可表示为
| A.1.1×1010 | B.11×1010 | C.1.1×109 | D.11×109 |
小明的讲义夹里放了大小相同的试卷共12页,其中语文4页、数学2页、英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为
A. |
B. |
C.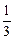 |
D.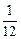 |
如图,直线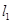 ∥
∥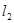 ,∠1=550,∠2=650,则∠3为
,∠1=550,∠2=650,则∠3为
| A.500. | B.550 | C.600 | D.650 |

下列正多边形的组合中,不能铺满地面的是
| A.正三角形和正五边形 | B.正三角形和正四边形 |
| C.正三角形和正十二边形 | D.正三角形和正六边形 |
下列说法中,①三角形的内角中最多有一个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引(n-3)条对角线,把n边形分成(n-2)个三角形,因此,n边形的内角和是(n-2)·1800;④六边形的对角线有7条,正确的个数有
| A.4个 | B.3个 | C.2个 | D.1个 |
下列轴对称图形中,对称轴条数最少的是
| A.等边三角形 | B.正方形 | C.正六边形 | D.圆 |
下列说法正确的是
| A.买一张福利彩票一定中奖,是必然事件. |
| B.买一张福利彩票一定中奖,是不可能事件. |
C.抛掷一个正方体骰子,点数为奇数的概率是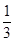 . . |
| D.一组数据:1,7,3,5,3的众数是3. |
有下列四个命题:
①对顶角相等;②两条直线被第三条直线所截,如果内错角相等,那么两直线平行;
③如果一个角的两边分别平行于另一个角的两边,那么这两个角相等;④圆有无数条直径。请把你认为是正确的说法的序号填在横线上___________________。
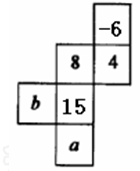
一个正方体的表面展开图如图所示,每一个面上都写有一个整数,并且相对两个面上所写的两个整数之和都相等,那么 ,
,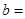 。
。
如图,正方形的边长为2,分别以正方形的两个相对顶点为圆心,以正方形的一边为半径画弧,则阴影部分的面积是 。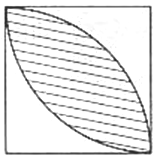
连续抛掷一枚质地均匀的硬币9次,落下后出现正面朝上的结果是8次,抛掷第10次时,落下后正面朝上的概率是_______。
正 边形的每一个外角都是900;如果一个正多边形的每一个内角都是与它相邻外角的3倍,那么这个正多边形的内角和是 。
小明玩一种游戏,每次挪动珠子的颗数与对应所得的分数如下表:
| 挪动珠子数(颗) |
2 |
3 |
4 |
5 |
6 |
…… |
| 对应所得分数(分) |
2 |
6 |
12 |
20 |
30 |
…… |
当每次挪动11颗珠子时,所得的分数是 分;当所得分数为72分时,则挪动的珠子数为 颗.
一个袋子里装有20个大小和质量相同的球,分别写有编号1至20.任意从中摸出1个球,这个球的编号能被5整除的概率是 ,这个球的编号大于10的概率是 。
(每小题5分,共10分) 计算:
(1)一个三角形底边的长是 ,高是
,高是 。如果将底边增加2,高减少2,,为了使面积不变,那么
。如果将底边增加2,高减少2,,为了使面积不变,那么 和
和 应满足什么关系?
应满足什么关系?
(2)已知等腰三角形的周长为20,若有一边长为4,,则另外两边的长分别是多少?
(每小题6分,共12分)
(1)如图,BD与CD分别平分 ∠ABC和∠ACB,已知∠BDC=
∠ABC和∠ACB,已知∠BDC= ,求∠A的度数。
,求∠A的度数。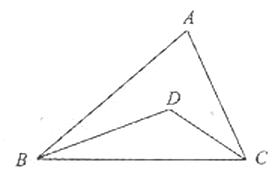
(2)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,求∠1的度数.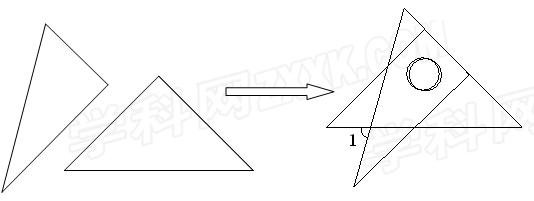
(满分8分)受气候等因素的影响,今年某些农产品的价格有所上涨. 张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元.其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.则甲、乙两种 蔬菜各种植了多少亩?
蔬菜各种植了多少亩?
(满分8分)在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x
轴,y轴分别交于A,B两点.
(1)求直线l的函数关系式;
(2)求△AOB的面积.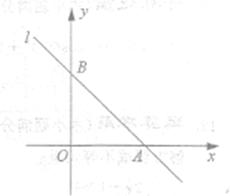
(满分10分)有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外 ,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你求出摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖 赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.









 ,则下列不等式成立的是( )
,则下列不等式成立的是( )




 ,其中正确的是( )
,其中正确的是( ) 
 是方程
是方程 的一个根,则
的一个根,则 的值为( )
的值为( )


 且
且 ,
, ,则
,则 的值为
的值为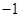
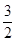




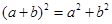
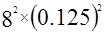 = ,
= ,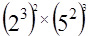 = .
= .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号