(每小题5分,共10分) 计算:
(1)一个三角形底边的长是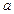 ,高是
,高是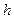 。如果将底边增加2,高减少2,,为了使面积不变,那么
。如果将底边增加2,高减少2,,为了使面积不变,那么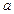 和
和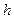 应满足什么关系?
应满足什么关系?
(2)已知等腰三角形的周长为20,若有一边长为4,,则另外两边的长分别是多少?
相关知识点
推荐套卷
(每小题5分,共10分) 计算:
(1)一个三角形底边的长是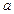 ,高是
,高是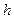 。如果将底边增加2,高减少2,,为了使面积不变,那么
。如果将底边增加2,高减少2,,为了使面积不变,那么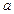 和
和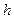 应满足什么关系?
应满足什么关系?
(2)已知等腰三角形的周长为20,若有一边长为4,,则另外两边的长分别是多少?