广东省东莞市教育局教研室高三上学期数学文卷
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为 的样本,其频率分布直方图如右图所示,其中支出在
的样本,其频率分布直方图如右图所示,其中支出在 元的同学有39人,则
元的同学有39人,则 的值为
的值为
| A.100 | B.120 | C.130 | D.390 |

把边长为 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,形成三棱锥
,形成三棱锥 的正视图与俯视图如右图所示,则侧视图的面积为
的正视图与俯视图如右图所示,则侧视图的面积为
A. |
B. |
C. |
D. |
将正方形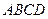 分割成
分割成
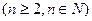 个全等的小正方形(图1,图2分别给出了
个全等的小正方形(图1,图2分别给出了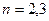 的情形),在每个小正方形的顶点各放置一个数,使位于正方形
的情形),在每个小正方形的顶点各放置一个数,使位于正方形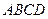 的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点
的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点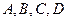 处的四个数互不相同且和为1,记所有顶点上的数之和为
处的四个数互不相同且和为1,记所有顶点上的数之和为 ,则
,则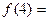
A.4 B.6 C.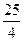 .
.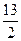

(几何证明选讲选做题) 如图,在 中,
中, ,
, ,
, ,以点
,以点 为圆心,线段
为圆心,线段 的长为半径的半圆交
的长为半径的半圆交 所在直线于点
所在直线于点 、
、 ,交线段
,交线段 于点
于点 ,则线段
,则线段 的长为 .
的长为 .
(坐标系与参数方程选做题)
已知圆 的参数方程为
的参数方程为 (
( 为参数).以原点为极点,
为参数).以原点为极点, 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,则直线
,则直线 与圆
与圆 的交点的直角坐标为 .
的交点的直角坐标为 .
(本小题满分 分)
分)
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.
规定评估的平均得分与全市的总体交通状况等级如下表:
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;
(2)用简单随机抽样方法从这 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的 绝对值不超过
绝对值不超过 的概率.
的概率.
(本小题满分14分)
在三棱锥 中,
中,
 是边长为
是边长为 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
, ,
, 、
、 分别为
分别为 、
、 的中点。
的中点。
(1)证明: ⊥
⊥ ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分 分)
分)
已知椭圆 的中心在坐标原点
的中心在坐标原点 ,两个焦点分别为
,两个焦点分别为 、
、 ,一个顶点为
,一个顶点为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)对于 轴上的点
轴上的点 ,椭圆
,椭圆 上存在点
上存在点 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)
已知函数
 满足
满足 .
.
(1)求 的值及函数
的值及函数 的单调区间;
的单调区间;
(2)若函数 在
在 内有两
内有两 个零点,求实数
个零点,求实数 的取值范围.
的取值范围.
 ,
, ,则
,则



 ,其中
,其中 是实数,
是实数, 是虚数单位,则
是虚数单位,则

 已知函数
已知函数 ,则函数
,则函数 的最小正周期是
的最小正周期是



 的一条渐近线方程为
的一条渐近线方程为 ,则该双曲线的离心率为
,则该双曲线的离心率为


 中,如果
中,如果 那么该数列的前
那么该数列的前 项和为
项和为




 点
点 在
在 上,
上, 
 . 则向量
. 则向量 等于
等于



 ,则
,则 .
.
 ,
, .若命题
.若命题 是假命题,则实数
是假命题,则实数 的取值范围是 .(用区间表示)
的取值范围是 .(用区间表示) ,在可行域内任取一点
,在可行域内任取一点 ,则点
,则点 满足
满足 的概率是 .
的概率是 . 分)
分) .
. 的最大值;
的最大值;
 中,
中, ,角
,角 满足
满足 ,求
,求 的各项满足:
的各项满足:
 ,
, .
. 是否成等比数列;
是否成等比数列; 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号