2013年全国统一高考理科数学试卷(北京卷)
已知集合 , ,则 = ( )
| A. | {0} | B. | {-1,0} | C. | {0,1} | D. | {-1,0,1} |
来源:2013年全国普通高等学校招生统一考试理科数学
" "是"曲线 过坐标原点的" ( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
来源:2013年全国普通高等学校招生统一考试理科数学
将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的两张参观券连号,那么不同的分法种数是.
来源:2013年全国普通高等学校招生统一考试理科数学
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天
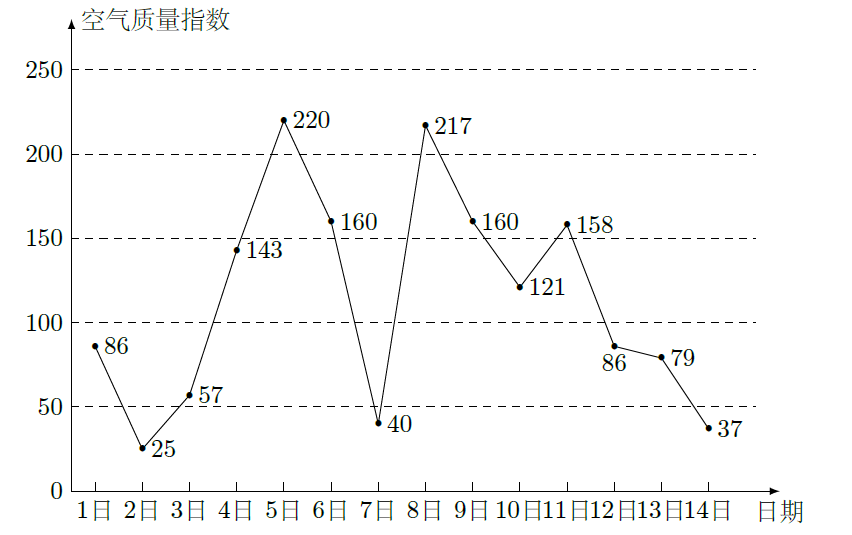
(Ⅰ)求此人到达当日空气重度污染的概率
(Ⅱ)设
是此人停留期间空气质量优良的天数,求
的分布列与数学期望.
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
来源:2013年全国普通高等学校招生统一考试理科数学
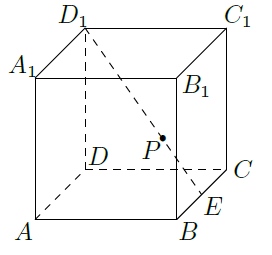
如图,在三棱柱
中,
是边长为4的正方形.平面
平面
,
.
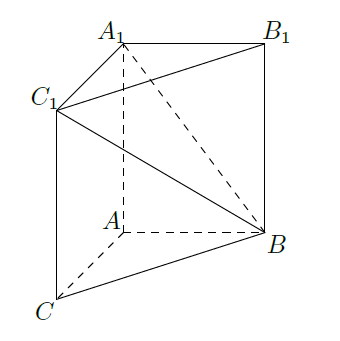
(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的余弦值;
(Ⅲ)证明:在线段
存在点
,使得
,并求
的值.
来源:2013年全国普通高等学校招生统一考试理科数学
设
为曲线
在点(1,0)处的切线.
(I)求
的方程;
(II)证明:除切点(1,0)之外,曲线
在直线
的下方.
来源:2013年全国普通高等学校招生统一考试理科数学
已知
是椭圆
上的三个点,
是坐标原点.
(I)当点
是
的右顶点,且四边形
为菱形时,求此菱形的面积.
(II)当点
不是
的顶点时,判断四边形
是否可能为菱形,并说明理由.
来源:2013年全国普通高等学校招生统一考试理科数学
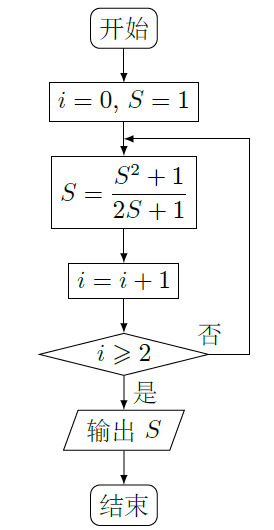
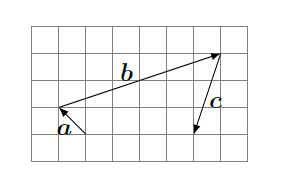
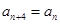 ),写出
,
,
,
的值;
),写出
,
,
,
的值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号