2013年全国统一高考文科数学试卷(福建卷)
设点 ,则 且 是"点 在直线 上"的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数 后,输出的 ,那么 的值为()

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
将函数 的图像向右平移 个单位长度后得到函数 的图像,若 的图像都经过点 ,则 的值可以是( )
| A. | B. | C. | D. |
已知
与
之间的几组数据如下表:
| 1 |
2 |
3 |
4 |
5 |
6 |
|
| 0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为 ,则以下结论正确的是()
| A. |
|
B. |
|
| C. |
|
D. |
|
设
是R的两个非空子集,如果存在一个从
到
的函数 ,(i)
(ii)对任意
,当
时,恒有
.那么称这两个集合"保序同构",现给出以下3对集合:
,(i)
(ii)对任意
,当
时,恒有
.那么称这两个集合"保序同构",现给出以下3对集合:
①    ②   ③
其中,"保序同构"的集合对的序号是.(写出"保序同构"的集合对的序号).
如图,在四棱柱 中, 平面 , , .

(1)当正视方向与向量
的方向相同时,画出四棱锥
的正视图(要求标出尺寸,并写出演算过程);
(2)若
为
的中点,求证:求二面角
.
(3)求三棱锥 的体积.
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在"25周岁以上(含25周岁)"和"25周岁以下"分为两组,再将两组工人的日平均生产件数分为5组: , , , , ,分别加以统计,得到如图所示的频率分布直方图.

(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名"25周岁以下组"工人的概率;
(II)规定日平均生产件数不少于80件者为"生产能手",请你根据已知条件完成列联表,并判断是否有90%的把握认为"生产能手与工人所在的年龄组有关"?
附: (注:此公式也可以写成 )
| 0.100 |
0.050 |
0.010 |
0.001 |
|
| 2.706 |
3.841 |
6.635 |
10.828 |
如图,抛物线
的焦点为
,准线
与
轴的交点为
.点
在抛物线
上,以
为圆心,
为半径作圆,设圆
与准线
交于不同的两点
,
.
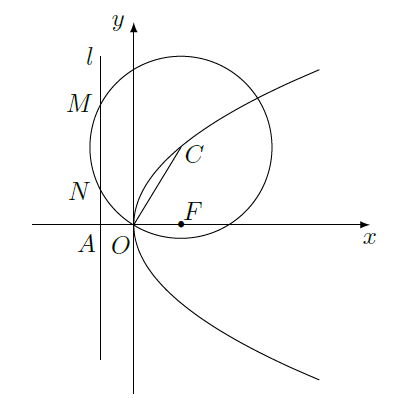
(I)若点
的纵坐标为2,求
;
(II)若
,求圆
的半径.
如图,在等腰直角
中,
,
,点
在线段
上.
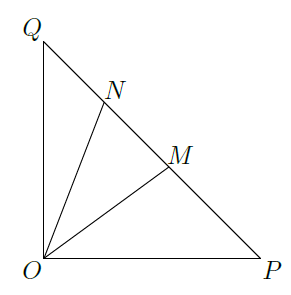
(Ⅰ) 若
,求
的长;
(Ⅱ)若点
在线段
上,且
,问:当
取何值时,
的面积最小?并求出面积的最小值.








 粤公网安备 44130202000953号
粤公网安备 44130202000953号