如图,在四棱柱 中, 平面 , , .
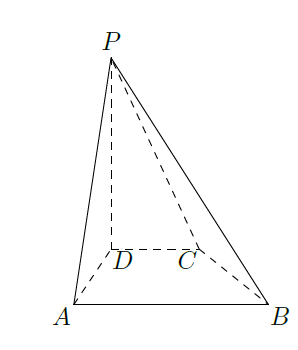
(1)当正视方向与向量
的方向相同时,画出四棱锥
的正视图(要求标出尺寸,并写出演算过程);
(2)若
为
的中点,求证:求二面角
.
(3)求三棱锥 的体积.
推荐套卷
如图,在四棱柱 中, 平面 , , .

(1)当正视方向与向量
的方向相同时,画出四棱锥
的正视图(要求标出尺寸,并写出演算过程);
(2)若
为
的中点,求证:求二面角
.
(3)求三棱锥 的体积.