江苏省高考预测试题数学
下列流程图(假设函数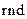 (0,1)是产生随机数的函数,它能
(0,1)是产生随机数的函数,它能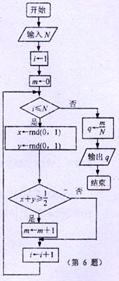
随机产生区间(0,1)内的任何一个实数)。随着输入N的不断
增大,输出的值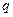 会在某个常数
会在某个常数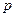 附近摆动并趋于稳定,则
附近摆动并趋于稳定,则
常数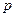 的值是 。
的值是 。
已知:以点 为圆心的圆与x轴交于点O,A,与Y轴交于点O,B,其中O为原点.
为圆心的圆与x轴交于点O,A,与Y轴交于点O,B,其中O为原点.
(1)求证:△OAB的面积为定值:
(2)设直线y=-2x+4与圆C交于点M,N,若OM= ON,求圆C的方程.
某产品按质最分成6种不同档次。假设工时不变,每天可生产最低档次40件。若每提高一个档次,每件利润增加1元,但是每天要少生产2件产品。
(1)若最低档次产品利润每件为16元时,问生产哪种档次产品每天所获利润最大?
(2)由于原材料价格的浮动,生产最低档次产品每什利润a [8,24]元,那么生产哪种档次产品利润最大?
[8,24]元,那么生产哪种档次产品利润最大?
设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的 ∈(O,1),
∈(O,1),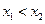 ,若f(
,若f(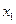 )≥f(
)≥f(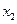 ),则(0,
),则(0,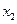 )为含峰区间:若f(
)为含峰区间:若f(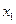 )
)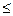 f(
f(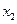 ),则
),则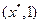 为含峰区间:
为含峰区间:
(II)对给定的r(0<r<0.5),证明:存在 ∈(0,1),满足
∈(0,1),满足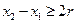 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:
(III)选取 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为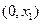 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取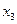 ,由
,由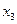 与
与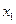 或
或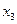 与
与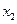 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,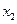 )的情况下,试确定的值
)的情况下,试确定的值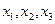 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
【必做题】(本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是‘‘海宝”,即可获奖,否则,均为不获奖.卡片用后后放同盒子,下一位参加者继续重复进行。
(I)有三人参加抽奖,要使至少一人获奖的概率不低于 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(2)若有四张“海宝”卡,现有甲乙丙丁四人依次抽奖.用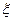 表示获奖的人数,求
表示获奖的人数,求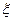 的分布列及E
的分布列及E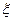 的值.
的值.
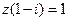 ,则复数
,则复数 在复平面上对应的点位于第 象限。
在复平面上对应的点位于第 象限。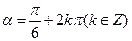 ”是“
”是“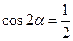 ”的 条件。
”的 条件。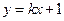 与曲线
与曲线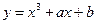 相切于点
相切于点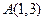 ,则
,则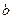 的值为 。
的值为 。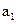 ,
,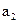 ,
,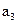 的方差是2,则样本2
的方差是2,则样本2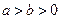 ,那么
,那么 的最小值是 。
的最小值是 。 ,
, ,
, ,…,
,…, 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,
是两个不重合的平面, ;②
;②
 ;④
;④
 在不等式
在不等式 表示的平面区域内部及其边界上运动,则
表示的平面区域内部及其边界上运动,则 的取值范围是 。
的取值范围是 。 内接于以
内接于以 为圆心半径为1的圆,且
为圆心半径为1的圆,且 ,则
,则 = 。
= 。 的右顶点
的右顶点 作斜率-1的直线,该直线与双曲线的两条渐近线的交点分别为
作斜率-1的直线,该直线与双曲线的两条渐近线的交点分别为 .若
.若 ,则双曲线的离心率是 。
,则双曲线的离心率是 。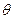 取遍所有值时,直线
取遍所有值时,直线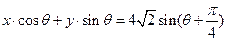 所围成的图形面积为
所围成的图形面积为 的方程
的方程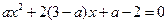 中的
中的 为负整数,则使方程至少有一个整数解时
为负整数,则使方程至少有一个整数解时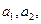 …,
…,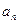 是各项不为零的
是各项不为零的 项等差数列,且公差
项等差数列,且公差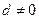 。若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对
。若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对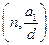 所组成的集合为 。
所组成的集合为 。 中,
中,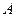 为锐角,角
为锐角,角 所对应的边分别为
所对应的边分别为 ,且
,且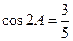 ,
, 。
。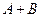 的值;
的值; ,求
,求 中,
中, ,
,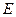 为
为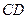 的中点,沿
的中点,沿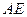 将
将 折起,使
折起,使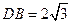 ,
,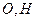 分别为
分别为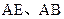 的中点。
的中点。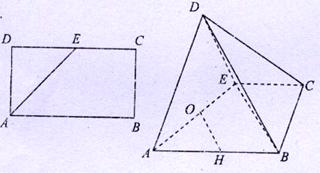
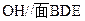

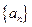 满足:
满足: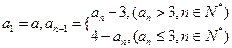
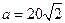 ,求数列
,求数列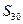 的值;
的值;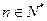 )时,
)时, 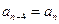 成立。
成立。 ,求矩阵A的特征向量及A2
,求矩阵A的特征向量及A2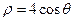 ,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线 的参数方程是:
的参数方程是: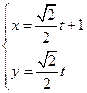 ,求直线
,求直线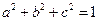 ,若
,若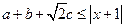 对任意实数a,b,c恒成立,求实数
对任意实数a,b,c恒成立,求实数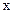 的取值范围。
的取值范围。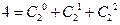 ,
, ,
,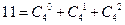 ;……
;…… 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分( 粤公网安备 44130202000953号
粤公网安备 44130202000953号