[江苏]2013届江苏省仪征市九年级第二次模拟考试数学试卷
为了解决迫在眉睫的环境问题,中国2013年预算案显示,中央和地方政府2013年将向节能和环境保护相关领域投入约32860000万元,将大力改善发电站的电力供应结构.近似数32860000用科学记数法可表示为( )
| A.3.286×105 | B.3.286×106 | C.3.286×107 | D.3.286×108 |
一个几何体的主视图和左视图都是正方形,俯视图是一个圆,那么这个几何体是( )
| A.长方体 | B.正方体 | C.圆锥 | D.圆柱 |
如果两圆的半径分别是 和
和 ,圆心距为
,圆心距为 ,那么这两圆的位置关系是( )
,那么这两圆的位置关系是( )
| A.相交 | B.内切 | C.外离 | D.外切 |
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C 的圆心坐标为(0,-1),半径为1.若 是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
A.3 B. C.
C. D.4
D.4
某工厂2010年、2011年、2012年的产值连续三年呈直线上升,具体数据如下表:
则2011年的产值为 .
| 年份 |
2010 |
2011 |
2012 |
| 产值 |
 |
|
 |
为了迎接全市体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的300名男生中随机抽取了部分男生的测试成绩(单位:米,精确到0.01米)作为样本进行分析,绘制了如图所示的频数分布直方图( 每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为 ,其中
,其中 这一小组的频数为8,请根据有关信息解答下列问题:
这一小组的频数为8,请根据有关信息解答下列问题:
(1)填空:这次调查的样本容量为 ,2.40~2.60这一小组的频率为 ;
(2)请指出样本成绩的中位数落在哪一小组内,并说明理由;
(3)样本中男生立定跳远的人均成绩最低值是多少米?
(4)请估计该校初三男生立定跳远成绩在2.00米以上(包括2.00米)的约有多少人?
现有形状、大小和颜色完全一样的三张卡片,上面分别标有数字“2”、“3”、“4”,第一次从这三张卡片中随机抽取一张,记下数字后放回,第二次再从这三张卡片中随机抽取一张并记下数字.
(1)请用列表或画树状图的方法表示出上述试验所有可能的结果;
(2)求两次抽取的数字之积不小于9的概率.
已知:如图所示, 为任意三角形,若将
为任意三角形,若将 绕点
绕点 顺时针旋转180° 得到
顺时针旋转180° 得到 .
.
(1)试猜想 与
与 有何关系?说明理由;
有何关系?说明理由;
(2)请给 添加一个条件,使旋转得到的四边形
添加一个条件,使旋转得到的四边形 为矩形,并说明理由.
为矩形,并说明理由.
某校为了深化课堂教学改革,现要配备一批A、B两种型号的小白板,经与销售商洽谈,搭成协议,购买一块A型小白板比一块B型小白板贵20元,且购5块A型小白板和4块B型小白板共需820元。
(1)求分别购买一块A型、B型小白板各需多少元?
(2)根据该校实际情况,需购A、B两种型号共60块,要求总价不超过5300元,且A型数量多于总数的 ,请通过计算,求出该校有几种购买方案?
,请通过计算,求出该校有几种购买方案?
(3)在(2)的条件下,学校为了节约开支,至少需花多少钱采购?
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线
轴的垂线 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时,  为直角三角形.
为直角三角形.
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点 重合),点
重合),点 、
、 (
( )、
)、 在同一条直线上.
在同一条直线上. ,
, ,
, ,
, ,
, .如图(2),
.如图(2), 从图(1)的位置出发,以
从图(1)的位置出发,以 的速度沿
的速度沿 向
向 匀速移动,在
匀速移动,在 移动的同时,点
移动的同时,点 从
从 的顶点
的顶点 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿 向点
向点 匀速移动.当
匀速移动.当 的顶点
的顶点 移动到
移动到 边上时,
边上时, 停止移动,点
停止移动,点 也随之停止移动.
也随之停止移动. 与
与 相交于点
相交于点 ,连接
,连接 ,设移动时间为
,设移动时间为
 .
.

(1)当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻 ,使面积
,使面积 最小?若存在,求出
最小?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻 ,使
,使 、
、 、
、 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)







 ,两条对角线的比是4:3,则这个菱形的面积是( )
,两条对角线的比是4:3,则这个菱形的面积是( )



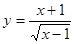 中自变量
中自变量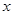 的取值范围是 .
的取值范围是 . .
. ,下底长是
,下底长是 ,则它的上底长是
,则它的上底长是  .
. ,则
,则 .
. 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ =56°,则∠
=56°,则∠ = 度.
= 度.
 的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .
的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .
 的方程
的方程 的解是正数,则
的解是正数,则 的取值范围为 .
的取值范围为 . 的面积为20,将
的面积为20,将 平移到
平移到 ,使
,使 和
和 重合,
重合,  交
交 于
于 ,则
,则 的面积为 .
的面积为 .

 ; (2) 化简:
; (2) 化简: .
. ; (2)解方程组:
; (2)解方程组: .
. 中,
中, ,
, .点
.点 为
为 边上一点,且
边上一点,且 ,
, .求△
.求△ .(结果保留根号)
.(结果保留根号)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号