2013年初中数学单元提优测试卷-多项式乘以多项式
在我们所学的课本中,多项式与多项式相称可以用几何图形的面积来表示,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用下面图中的图①来表示.请你根据此方法写出图②中图形的面积所表示的代数恒等式: .
把(x2﹣x+1)6展开后得a12x12+a11x11+…a2x2+a1x1+a0,则a12+a10+a8+a6+a4+a2+a0= .
(2x6﹣3x5+4x4﹣7x3+2x﹣5)(3x5﹣3x3+2x2+3x﹣8)展开式中x8的系数是 .
已知x、y、a都是实数,且|x|=1﹣a,y2=(1﹣a)(a﹣1﹣a2),则x+y+a3+1的值为 .
设x*y定义为x*y=(x+1)(y+1),x*2定义为x*2=x*x,则多项式3*(x*2)﹣2*x+1,当x=2时的值为 .
我们知道多项式的乘法可以利用图形的面积进行解释,如(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示:
(1)请你写出图3所表示的一个等式: .
(2)试画出一个图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.
如图,有足够多的边长为a的大正方形、长为a宽为b的长方形以及边长为b的小正方形.(1)取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(a+b)(a+2b),画出图形,并根据图形回答(a+b)(a+2b)= .
(2)取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+4b2,
①需要A类卡片 张、B类卡片 张、C类卡片 张.
②可将多项式a2+5ab+4b2分解因式为 .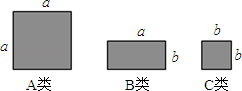
小明在进行两个多项式的乘法运算时(其中的一个多项式是b﹣1),把“乘以(b﹣1)”错看成“除以(b﹣1)”,结果得到(2a﹣b),请你帮小明算算,另一个多项式是多少?
若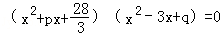 的积中不含x2与x3项,
的积中不含x2与x3项,
(1)求p、q的值;
(2)求代数式(﹣2p2q)3+(3pq)﹣1+p2010q2012的值.
填空(x﹣y)(x2+xy+y2)= ;(x﹣y)(x3+x2y+xy2+y3)=
根据以上等式进行猜想,当n是偶数时,可得:(x﹣y)(xn+xn﹣1y+yn﹣2y2+…+x2yn﹣2+xyn﹣1+yn)= .
已知p,q满足代数式(x2+px+8)(x2﹣3x﹣q)的展开始终不含有x2和x3项,求p,q的值.
计算下列各式,然后回答问题:(x+3)(x+4)= ;(x+3)(x﹣4)= ;(x﹣3)(x+4)= ;(x﹣3)(x﹣4)= .
(1)根据以上的计算总结出规律:(x+m)(x+n)= ;
(2)运用(1)中的规律,直接写出下列结果:(x+25)(x﹣16)= .
(x2+x+1)(x+2)
(x2﹣x﹣1)(x+1)
(x2+2x﹣1)(x﹣1)
(x2﹣2x+3)(x﹣2)
(a2+3a﹣2)(a+3)
(a2﹣3a+4)(a﹣3)
(a2+4a+1)(2a﹣1)
(a2﹣4a+2)(3a+2)
(2x2﹣3)(x+5)
甲乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;由于乙漏抄了第二个多项中的x的系数,得到的结果为2x2﹣9x+10.请你计算出a、b的值各是多少,并写出这道整式乘法的正确结果.
已知6x2﹣7xy﹣3y2+14x+y+a=(2x﹣3y+b)(3x+y+c),试确定a、b、c的值.
一个二次三项式x2+2x+3,将它与一个二次项ax+b相乘,积中不出现一次项,且二次项系数为1,求a,b的值?
如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积.
阅读下列解答过程,并回答问题.
在(x2+ax+b)(2x2﹣3x﹣1)的积中,x3项的系数为﹣5,x2项的系数为﹣6,求a,b的值.
解:(x2+ax+b)•(2x2﹣3x﹣1)=
2x4﹣3x3+2ax3+3ax2﹣3bx=①
2x4﹣(3﹣2a)x3﹣(3a﹣2b)x2﹣3bx ②
根据对应项系数相等,有 ,解得
,解得
回答:
(1)上述解答过程是否正确? .
(2)若不正确,从第 步开始出现错误,其他步骤是否还有错误? .
(3)写出正确的解答过程.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号