2008年全国统一高考理科数学试卷（安徽卷）

集合 $A=\left\{y\in R|y=lgx,x>1\right\}$ ， $B=\left\{-2,-1,1,2\right\}$ 则下列结论正确的是（  ）

若过点 $A(4,0)$的直线 $l$与曲线 $(x-2{)}^2+y^2=1$有公共点，则直线 $l$的斜率的取值范围为（   ）

在同一平面直角坐标系中，函数 $y=g\left(x\right)$的图象与 $y=e^x$的图象关于直线 $y=x$对称。而函数 $y=f\left(x\right)$的图象与 $y=g\left(x\right)$的图象关于 $y$轴对称，若 $f\left(m\right)=-1$，则 $m$的值是（  ）

设两个正态分布 $N({\mu }_1,{{\sigma }_1}^2)({\sigma }_1>0)$ 和 $N({\mu }_2,{{\sigma }_2}^2)({\sigma }_2>0)$ 的密度函数图像如图所示.则有（   ）

若函数 $f\left(x\right),g\left(x\right)$分别是 $R$上的奇函数、偶函数，且满足 $f\left(x\right)-\left(x\right)\equiv e^x$，则有（）

12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的总数是(   )

函数 $f\left(x\right)=\frac{\sqrt{\left|x-2\right|-1}}{{\log }_2\left(x-1\right)}$的定义域为．

为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物。某人一次种植了 $n$株沙柳，各株沙柳成活与否是相互独立的，成活率为 $p$，设 $\xi$为成活沙柳的株数，数学期望 $E\xi =3$，标准差 $\sigma \xi$为 $\frac{\sqrt{6}}{2}$.
（Ⅰ）求 $n,p$的值并写出 $\xi$的分布列；
（Ⅱ）若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率.

设函数 $f\left(x\right)=\frac{1}{x\ln x}(x>0且x\ne 1)$

（Ⅰ）求函数 $f\left(x\right)$的单调区间；
（Ⅱ）已知 $2^{\frac{1}{x}}>x^2$对任意 $x\in (0,1)$成立，求实数 $a$的取值范围。

设数列 $\left\{a_n\right\}$满足 $a_0=0,a_{n+1}=c{a_n}^3+1-c,c\in N^{*}$,其中 $c$为实数.
（Ⅰ）证明： $a_n\in [0,1]$对任意 $n\in N^{*}$成立的充分必要条件是 $c\in [0,1]$.

（Ⅱ）设 $0<c<\frac{1}{3}$，证明： $a_n\ge 1-(3c{)}^{n-1},n\in N^{*}$;
（Ⅲ）设 $0<c<\frac{1}{3}$，证明： ${a_1}^2+{a_2}^2+....+{a_n}^2>n+1-\frac{2}{1-3c},n\in N^{*}$

设椭圆 $C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)$过点 $M\left(\sqrt{2},1\right)$，且左焦点为 $F_1\left(-\sqrt{2},0\right)$

（Ⅰ）求椭圆 $C$的方程；
（Ⅱ）当过点 $P\left(4,1\right)$的动直线 $l$与椭圆 $C$相交与两不同点 $A,B$时，在线段 $AB$上取点 $Q$，满足 $\left|\stackrel{\rightharpoonup }{AP}\right|=\left|\stackrel{\rightharpoonup }{QB}\right|=\left|\stackrel{\rightharpoonup }{AQ}\right|=\left|\stackrel{\rightharpoonup }{PB}\right|$，证明：点 $Q$总在某定直线上.

设 ${\left(1+x\right)}^8=a_0+a_{1}x+\cdots +a_8{x}^8$,则 $a_0,a_1,\cdots ,a_8$中奇数的个数为（）

已知函数 $f\left(x\right)=\cos \left(2x-\frac{\pi }{3}\right)+2\sin \left(x-\frac{\pi }{4}\right)\sin \left(x+\frac{\pi }{4}\right)$

（Ⅰ）求函数 $f\left(x\right)$的最小正周期和图象的对称轴方程
（Ⅱ）求函数 $f\left(x\right)$在区间 $\left[-\frac{\pi }{12},\frac{\pi }{2}\right]$上的值域

在数列 $\left\{a_n\right\}$在中， $a_n=4n-\frac{5}{2},a_1+a_2+.....+a_n=a{n}^2+bn,n\in N*$,其中 $a,b$为常数，则 $\underset{n\to \infty }{lim}\frac{a^n-b^n}{a^n+b^n}$的值是   .

复数 $i^2(1+i{)}^2=$（）

将函数 $y=\sin (2x+\frac{\pi }{3})$的图象按向量 $a$平移后所得的图象关于点 $(-\frac{\pi }{12},0)$中心对称，则向量 $a$的坐标可能为（  ）

如图，在四棱锥 $O-ABCD$中，底面 $ABCD$四边长为1的菱形， $\angle ABC=\frac{\pi }{4}$, $OA\perp$底面 $ABCD$, $OA=2$, $M$为 $OA$的中点， $N$为 $BC$的中点.

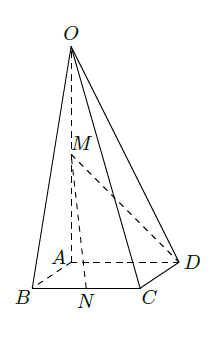
（Ⅰ）证明：直线 $MN//$平面 $OCD$ ；
（Ⅱ）求异面直线 $AB$与 $MD$所成角的大小；
（Ⅲ）求点 $B$到平面 $OCD$的距离.

在平行四边形 $ABCD$中， $AC$为一条对角线，若 $\stackrel{\rightharpoonup }{AB}=\left(2,4\right)$， $\stackrel{\rightharpoonup }{AC}=\left(1,3\right)$,则 $\stackrel{\rightharpoonup }{BD}=$（）

已知点 $A.B.C,D$在同一个球面上， $AB\perp$平面 $BCD$， $BC\perp CD$，若 $AB=6$，
$AC=2\sqrt{13}$， $AD=8$，则 $B,C$两点间的球面距离是．

已知 $m,n$是两条不同直线， $\alpha ,\beta ,\gamma$是三个不同平面，下列命题中正确的是（  ）

$a<0$是方程 $a{x}^2+2x+1=0$至少有一个负数根的（ ）

若 $A$为不等式组 $\left\{\begin{array}{c}x\le 0\\ y\ge 0\\ y-x\le 2\end{array}\right.$表示的平面区域，则当 $a$从－2连续变化到1时，动直线 $x+y=a$扫过 $A$中的那部分区域的面积为。