高考常见试题易错点点睛系列--平面解析几何
已知P为抛物线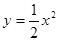 上的动点,点P在x轴上的射影为M,点A的坐标是
上的动点,点P在x轴上的射影为M,点A的坐标是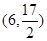 ,则
,则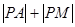 的最小值是( )
的最小值是( )
| A.8 | B.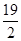 |
C.10 | D.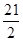 |
来源:高考常见试题易错点点睛系列--平面解析几何
已知双曲线C 2x2-y2=2与点P(1,2)
(1)求过P(1,2)点的直线l的斜率取值范围,使l与C分别有一个交点,两个交点,没有交点
(2)若Q(1,1),试判断以Q为中点的弦是否存在
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件 |F2A|、|F2B|、|F2C|成等差数列(1)求该弦椭圆的方程;(2)求弦AC中点的横坐标;(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围 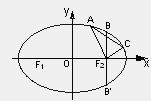
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为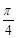 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积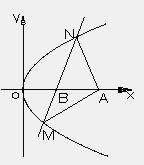
已知正方形ABCD 对角线AC所在直线方程为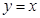 .抛物线
.抛物线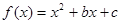 过B,D两点
过B,D两点
(1)若正方形中心M为(2,2)时,求点N(b,c)的轨迹方程。
(2)求证方程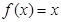 的两实根
的两实根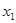 ,
,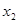 满足
满足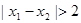
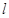 过点,那么直线
过点,那么直线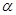 的取值范围是( )。
的取值范围是( )。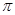 )
)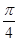 ]
] [
[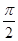 ,
, 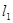 和
和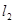 夹角的平分线为
夹角的平分线为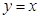 ,若
,若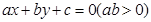 ,则
,则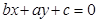
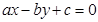
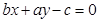
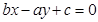
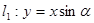 和直线
和直线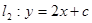 ,则直线
,则直线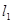 与
与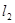 ( )。
( )。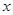 轴围成等腰直角三角形
轴围成等腰直角三角形 轴的正方向成
轴的正方向成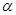 角,遇
角,遇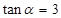 ,则反射光线所在的直线方程为( )
,则反射光线所在的直线方程为( )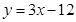
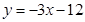
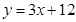
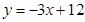
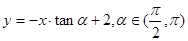 的倾斜角是( )。
的倾斜角是( )。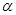
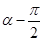
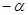
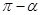
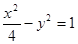 的两个焦点,点在双曲线上且满足
的两个焦点,点在双曲线上且满足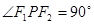 ,则
,则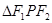 的面积是( )。
的面积是( )。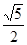
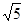
 ,当
,当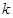 变化时,直线被椭圆
变化时,直线被椭圆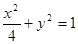 截得的最大弦长是( )
截得的最大弦长是( )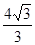
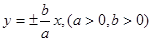 ,若双曲线上有一点M(
,若双曲线上有一点M(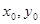 ),使
),使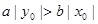 ,那双曲线的交点( )。
,那双曲线的交点( )。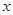 轴上
轴上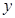 轴上
轴上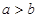 时在
时在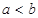 时在
时在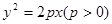 的焦点作一条直线交抛物线于
的焦点作一条直线交抛物线于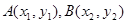 ,则
,则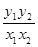 为( )
为( )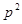
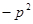
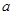 ,0)作椭圆
,0)作椭圆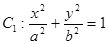 的弦,弦中点的轨迹仍是椭圆,记为
的弦,弦中点的轨迹仍是椭圆,记为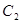 ,若
,若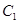 和
和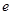 和
和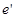 ,则
,则 的直线
的直线 与
与 轴正半轴、
轴正半轴、 轴正半轴分别交于
轴正半轴分别交于 、
、 两点,则
两点,则 的面积最小为 .
的面积最小为 . 上有一点P到左准线的距离为
上有一点P到左准线的距离为 ,则P到右焦点的距离为 。
,则P到右焦点的距离为 。 有共同焦点,并且与其中一个交点的纵坐标为4,则这个双曲线的方程为_____。
有共同焦点,并且与其中一个交点的纵坐标为4,则这个双曲线的方程为_____。 上,求
上,求 的最大、最小值.
的最大、最小值. ,右焦点
,右焦点 ,离心率
,离心率 ,求双曲线方程.
,求双曲线方程. 在轴上,离心率
在轴上,离心率 ,已知点
,已知点 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是 ,求这个椭圆的方程.
,求这个椭圆的方程. 与直线L:
与直线L: 仅有一个公共点,求m的范围.
仅有一个公共点,求m的范围.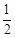 ,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。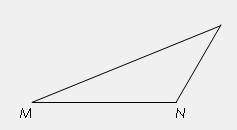
 粤公网安备 44130202000953号
粤公网安备 44130202000953号