[河北]2013届河北省五校联盟高三上学期调研考试文科数学试卷
等差数列 的前n项和为
的前n项和为 ,且9
,且9 ,3
,3 ,
, 成等比数列. 若
成等比数列. 若 =3,则
=3,则 = ( )
= ( )
| A.7 | B.8 | C.12 | D.16 |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( ) 
A. |
B. |
C. |
D. |
执行如图所示的程序框图,若输出的是 ,则输入整数
,则输入整数 的最小值是 ( )
的最小值是 ( )
| A.7 | B.8 | C.15 | D.16 |
下列结论错误的是( )
A.命题:“若 ”的逆否命题为:“若 ”的逆否命题为:“若 ,则 ,则 ” ” |
B.命题:“存在 为实数, 为实数, ”的否定是“任意 ”的否定是“任意 是实数, 是实数, ” ” |
C.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
| D.若p且q为假命题,则p、q均为假命题 |
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若 ;
;
②若 ;
;
③若 ;
;
④若m、n是异面直线,
其中真命题是( )
| A.①和② | B.①和③ | C.①和④ | D.③和④ |
已知点P为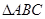 所在平面上的一点,且
所在平面上的一点,且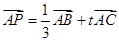 ,其中
,其中 为实数,若点P落在
为实数,若点P落在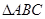 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )
A. |
B.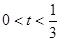 |
C.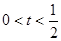 |
D.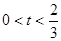 |
.已知三棱锥 的所有棱长均为2,D是SA 的中点,E是BC 的中点,则
的所有棱长均为2,D是SA 的中点,E是BC 的中点,则 绕直线SE 转一周所得到的旋转体的表面积为 .
绕直线SE 转一周所得到的旋转体的表面积为 .
(本小题满分12分) 锐角 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为 、
、 、
、 ,且
,且 .
.
(1)若 ,求角A、B、C大小;
,求角A、B、C大小;
(2)已知向量 ,
, ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下:
(1)现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;
(2)若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.
(本小题满分12分)如图,在四面体 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)若平面 ⊥平面
⊥平面 ,且
,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
.(本小题满分12分)已知椭圆的中心在原点,焦点在 轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)是否存在斜率为 ,且过定点
,且过定点 的直线
的直线 ,使
,使 与椭圆交于两个不同的点
与椭圆交于两个不同的点 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
② 是偶函数;
是偶函数;
③ 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设 ,求函数
,求函数 在
在 上的最小值.
上的最小值.
(本小题满分10分)选修4-1:几何证明选讲如图所示,已知 与⊙
与⊙ 相切,
相切, 为切点,
为切点, 为割线,弦
为割线,弦 ,
, 、
、 相交于
相交于 点,
点, 为
为 上一点,且
上一点,且 ·
·

(1)求证: ;
;
(2)求证: ·
· =
= ·
· .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为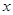 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线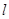 的参数方程是:
的参数方程是: (
( 是参数).
是参数).
(1)将曲线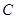 的极坐标方程和直线
的极坐标方程和直线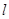 参数方程转化为普通方程;
参数方程转化为普通方程;
(2)若直线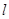 与曲线
与曲线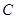 相交于A、B两点,且
相交于A、B两点,且 ,试求实数
,试求实数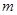 值.
值.
 ,B=
,B= ,则
,则 =( )
=( ) 



 (
( 为虚数单位)则
为虚数单位)则 ( )
( ) 


 ,点P的坐标为 ( )
,点P的坐标为 ( )



 则
则 ( )
( )



 的左顶点为
的左顶点为 ,右焦点为
,右焦点为 ,
, 为双曲线右支上一点,则
为双曲线右支上一点,则 最小值为( )
最小值为( )



 是偶函数,且
是偶函数,且 上是增函数,如果
上是增函数,如果 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是( )
的取值范围是( )



 关于直线
关于直线 对称的圆的方程为 ;
对称的圆的方程为 ;  满足不等式组
满足不等式组 ,则
,则 的最小值为 ;
的最小值为 ;  ,且关于
,且关于 的方程
的方程 有且只有一个实根,则实数
有且只有一个实根,则实数 的取值范围是 ;
的取值范围是 ;
 ;
; 的不等式
的不等式 的解集不是空集,求
的解集不是空集,求 得取值范围.
得取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号