[四川]2012届四川省资阳市高三第二次高考模拟考试理科数学试卷
已知集合 ,
, ,则
,则
| A.{x|7≤x<10} | B.{x|2<x≤3} |
| C.{x|2<x≤3或7≤x<10} | D.{x|2<x<3或7<x<10} |
“ ”是“
”是“ ”成立的
”成立的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知底面边长为2,侧棱长为 的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
A. |
B. |
C. |
D. |
某厂拟生产甲、乙两种适销产品,每件销售收入分别为0.3万元、0.2万元.甲、乙两种产品都需在A、B两种设备上加工,在每台A、B设备上加工1件甲产品设备所需工时分别为1 h、2 h,加工1件乙产品设备所需工时分别为2 h、1 h,A、B两种设备每月有效使用台时数分别为400 h、500 h.则月销售收入的最大值为
(A)50万元 (B)70万元 (C)80万元 (D)100万元
已知 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有 ,当
,当
 时,
时, ,则函数
,则函数 在区间
在区间 上的反函数
上的反函数 的值
的值
A. |
B. |
C. |
D. |
设F为抛物线 的焦点,A、B、C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA、△OFB、△OFC的面积分别为S1、S2、S3,则
的焦点,A、B、C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA、△OFB、△OFC的面积分别为S1、S2、S3,则
| A.9 | B.6 | C.3 | D.2 |
已知集合 ,
, ,定义函数
,定义函数 ,点
,点 、
、 、
、 ,点E为AC的中点,若△ABC的内切圆的圆心为D,且满足
,点E为AC的中点,若△ABC的内切圆的圆心为D,且满足 (
( ),则满足条件的函数个数是
),则满足条件的函数个数是
| A.16个 | B.12个 | C.10个 | D.6个 |
在正方体ABCD-A1B1C1D1中,E、F是分别是棱A1B1、A1D1的中点,则A1B与EF所成角的大小为__________
如图,已知F1、F2是椭圆 (
( )的左、右焦点,点P在椭圆C上,线段PF2与圆
)的左、右焦点,点P在椭圆C上,线段PF2与圆 相切于点Q,且点Q为线段PF2的中点,则椭圆C的离心率为________.
相切于点Q,且点Q为线段PF2的中点,则椭圆C的离心率为________.
已知函数 ,函数
,函数 (
( ,且mp<0),给出下列结论:
,且mp<0),给出下列结论:
①存在实数r和s,使得 对于任意实数x恒成立;
对于任意实数x恒成立;
②函数 的图像关于点
的图像关于点 对称;
对称;
③函数 可能不存在零点(注:使关于x的方程
可能不存在零点(注:使关于x的方程 的实数x叫做函数
的实数x叫做函数 的零点);
的零点);
④关于x的方程 的解集可能为{-1,1,4,5}.
的解集可能为{-1,1,4,5}.
其中正确结论的序号为 (写出所有正确结论的序号).
△ABC中,角A、B、C对边分别是a、b、c,满足 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
甲袋中装有大小相同的红球1个,白球2个;乙袋中装有与甲袋中相同大小的红球2个,白球3个.先从甲袋中取出1个球投入乙袋中,然后从乙袋中取出2个小球.
(Ⅰ)求从乙袋中取出的2个小球中仅有1个红球的概率;
(Ⅱ)记从乙袋中取出的2个小球中白球个数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
(Ⅰ)求证:EF⊥平面BCD;
(Ⅱ)求二面角C-DE-A的大小;
(Ⅲ)求点A到平面CDE的距离.
已知数列 的前n项和为
的前n项和为 ,
, ,且
,且 (
( ),数列
),数列 满足
满足 ,
, ,对任意
,对任意 ,都有
,都有 .
.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)令 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.
已知双曲线W: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,点
,点 ,右顶点是M,且
,右顶点是M,且 ,
, .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点 的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点
的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点 在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.





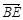
 中,若
中,若 ,
,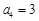 ,则该数列前五项的积为
,则该数列前五项的积为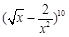 展开式中的常数项是
展开式中的常数项是 的图象不相交的一条直线是
的图象不相交的一条直线是



 __________
__________ ,函数
,函数 (其中
(其中 ,e是自然对数的底数).
,e是自然对数的底数). 时,求函数
时,求函数 的极值;
的极值; 在
在 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围; ,求证:
,求证: (其中e是自然对数的底数).
(其中e是自然对数的底数). 粤公网安备 44130202000953号
粤公网安备 44130202000953号