[江西]2011-2012学年江西省六校高三联考数学理科试卷
若集合A={y|y=x2-1},B={x| |x2-1| 3},则A
3},则A =( )
=( )
A. |
B.[-1,2] | C.[1,2] | D.[-2,-1] |
已知命题p:“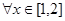 都有x2
都有x2 a”。命题q:“
a”。命题q:“ ,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )
,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )
A.a |
B.-2<a<1 | C.a≤-2或a=1 | D.a |
已知△ABC的三边a, b, c的长均为正整数,且a ,若b为常数,则满足条件的△ABC的个数是( )
,若b为常数,则满足条件的△ABC的个数是( )
| A.b2 | B. |
C. |
D. b b |
如果空间三条直线a, b, c两两成异面直线,那么与a, b, c都相交的直线有( )
| A.0条 | B.1条 | C.多于1条但为有限条 | D.无数条 |
已知点P(x, y)满足 =1,且F1(-3,0),F2(3, 0),则下列式子正确的为( )
=1,且F1(-3,0),F2(3, 0),则下列式子正确的为( )
A. |
B. |
C. |
D. |
已知集合A="{1," 2, 3, 4},函数f(x)的定义域、值域都是A,且对于任意 ,
, ,设
,设 1,
1,  2,
2,  3,
3,  4是1,2,3,4的任意一个排列,定义数表
4是1,2,3,4的任意一个排列,定义数表




 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )
| A.216 | B.108 | C.48 | D.24 |
设函数f(x)= (
( >0, 且
>0, 且
 1),[m]表示不超过实数m的最大整数,则函数[f(x)
1),[m]表示不超过实数m的最大整数,则函数[f(x) ]+[f
]+[f ]的值域是( )
]的值域是( )
A.{- , ,  } } |
B.{-1, 0} | C.{-1, 1} | D.{0} |
①在极坐标系中,点A(2, )到直线
)到直线 :
: 的距离为
的距离为
②(不等式选讲选做题) 设函数f(x)=|x-2|+x,g(x)=|x+1|,则g(x)<f(x)成立时x的取值范围
在△ABC中,A、B、C的对边分别为a、b、c,向量 ,
, ,若
,若 .
.
(1)求角A的大小;
(2)若 ,且
,且 ,求△ABC的面积
,求△ABC的面积
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数:  ,
, ,
, ,
, ,
, ,
,
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.
(1)求证:VD∥平面EAC;
(2)求二面角A—VB—D的余弦值.
设集合W是满足下列两个条件的无穷数列{an}的集合:
① ②
② ,其中n∈N*,M是与n无关的常数
,其中n∈N*,M是与n无关的常数
(1)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,试探究{Sn}与集合W之间的关系;
(2)设数列{bn}的通项为bn=5n-2n,且{bn}∈W,M的最小值为m,求m的值;
(3)在(2)的条件下,设 ,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
已知椭圆的中心在原点,准线方程为x=±4,如果直线 :3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
(1)求椭圆方程;
(2)设直线 与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
(3)把(2)的情况作一推广:写出命题(不要求证明)
 的虚部为( )
的虚部为( )






 +
+ ,x
,x 的大致图象为( )
的大致图象为( )
 ,
, 且
且 ∥
∥ ,则锐角
,则锐角 为 。
为 。
 , b的等差中项是
, b的等差中项是 ,等比中项为2
,等比中项为2 ,且
,且 =1的离心率为 。
=1的离心率为 。
 .
. ,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证:
,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证: ;
; 时,
时, (x>0)的最小值;
(x>0)的最小值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号