已知椭圆的中心在原点，准线方程为x=±4，如果直线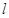
：3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点．
(1)求椭圆方程；
(2)设直线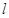与椭圆的一个交点为P，F是椭圆的一个焦点，试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系；
(3)把(2)的情况作一推广：写出命题（不要求证明）
相关试题
．
的单调区间；
上的最值．
．
的单调区间；
与函数
的图像有
个交点，求
的取值范围．
，若z2＋
z＋b＝1＋i，求实数
单调减区调为
，求函数
图象过点
的切线方程；
，使关于
的不等式
成立，求实数
取值范围．
的离心率
，它的一个焦点与抛物线
的焦点重合，过椭圆右焦点
作与坐标轴不垂直的直线
，交椭圆于
两点．
，且
，求直线推荐套卷
已知椭圆的中心在原点，准线方程为x=±4，如果直线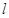：3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点．
(1)求椭圆方程；
(2)设直线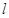与椭圆的一个交点为P，F是椭圆的一个焦点，试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系；
(3)把(2)的情况作一推广：写出命题（不要求证明）
粤公网安备 44130202000953号