[吉林]2012届吉林省长春市高三第一次调研测试理科数学试卷
“ ”是“函数
”是“函数 在区间
在区间 上存在零点”的
上存在零点”的
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列四个命题:
是两个不同的平面,则下列四个命题:
①若a⊥b,a⊥α,b α,则b∥α; ②若a∥α,a⊥β,则α⊥β;
α,则b∥α; ②若a∥α,a⊥β,则α⊥β;
③若a⊥β,α⊥β,则a∥α或a α; ④若a⊥b,a⊥α,b⊥β,则α⊥β.
α; ④若a⊥b,a⊥α,b⊥β,则α⊥β.
其中正确命题的个数为
| A.1 | B.2 | C.3 | D.4 |
一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为
A. |
B. |
C. |
D. |
函数 为奇函数,该函数的部分图像如图所示,
为奇函数,该函数的部分图像如图所示, 、
、 分别为最高点与最低点,且
分别为最高点与最低点,且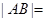
 ,则该函数图象的一条对称轴为
,则该函数图象的一条对称轴为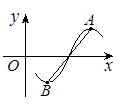
A. |
B.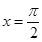 |
C. |
D. |
在△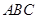 中,
中, 是
是 边中点,角
边中点,角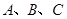 的对边分别是
的对边分别是 ,若
,若 ,则△
,则△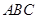 的形状为
的形状为
| A.直角三角形 | B.钝角三角形 |
| C.等边三角形 | D.等腰三角形但不是等边三角形 |
类比“两角和与差的正弦公式”的形式,对于给定的两个函数: ,
, ,其中
,其中 ,且
,且 ,下面正确的运算公式是
,下面正确的运算公式是
① ; ②
; ② ;
;
③2 ; ④2
; ④2 .
.
| A.①② | B.③④ | C.①④ | D.②③ |
设 、
、 分别为具有公共焦点
分别为具有公共焦点 、
、 的椭圆和双曲线的离心率,
的椭圆和双曲线的离心率, 是两曲线的一个公共点,且满足
是两曲线的一个公共点,且满足 ,则
,则 的值为
的值为
A. |
B.2 | C. |
D.1 |
设 是定义在
是定义在 上的增函数,且对于任意的
上的增函数,且对于任意的 都有
都有 恒成立. 如果实数
恒成立. 如果实数 满足不等式组
满足不等式组 ,那么
,那么 的取值范围是
的取值范围是
| A.(3, 7) | B.(9, 25) | C.(13, 49) | D.(9, 49) |
已知函数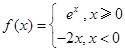 ,则关于
,则关于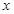 的方程
的方程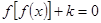 给出下列四个命题:
给出下列四个命题:
①存在实数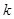 ,使得方程恰有1个实根;
,使得方程恰有1个实根;
②存在实数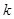 ,使得方程恰有2个不相等的实根;
,使得方程恰有2个不相等的实根;
③存在实数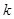 ,使得方程恰有3个不相等的实根;
,使得方程恰有3个不相等的实根;
④存在实数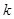 ,使得方程恰有4个不相等的实根.
,使得方程恰有4个不相等的实根.
其中正确命题的序号是 (把所有满足要求的命题序号都填上)
(本小题满分12分)
如图,在平面直角坐标系中,锐角 和钝角
和钝角 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
, 两点.
两点.
⑴如果 、
、 两点的纵坐标分别为
两点的纵坐标分别为 、
、 ,求
,求 和
和 ;
;
⑵在⑴的条件下,求 的值;
的值;
⑶已知点
 ,求函数
,求函数 的值域.
的值域.
(本小题满分12分)
如图,在底面为直角梯形的四棱锥 中
中 ,
, 平面
平面 ,
, ,
, ,
, .
.
⑴求证:
 ;
;
⑵求直线 与平面
与平面 所成的角;
所成的角;
⑶设点 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.
(本小题满分12分)
已知点 ,
, ,动点
,动点 的轨迹曲线
的轨迹曲线 满足
满足 ,
, ,过点
,过点 的直线交曲线
的直线交曲线 于
于 、
、 两点.
两点.
(1)求 的值,并写出曲线
的值,并写出曲线 的方程;
的方程;
(2)求△ 面积的最大值.
面积的最大值.
(本小题满分12分)
已知函数 .
.
⑴求函数 的最小值;
的最小值;
⑵若 ≥0对任意的
≥0对任意的 恒成立,求实数a的值;
恒成立,求实数a的值;
⑶在⑵的条件下,证明: .
.
(本小题满分10分)选修4-1:几何证明选讲.
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
(本小题满分10分)选修4-4:坐标系与参数方程选讲.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为 .
.
⑴求圆C的极坐标方程;
⑵ 是圆
是圆 上一动点,点
上一动点,点 满足
满足 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
 ,
, ,则?R
,则?R 等于
等于



 在复平面内对应的点在
在复平面内对应的点在 轴负半轴上,则实数
轴负半轴上,则实数 的值是
的值是



 的值为
的值为




 中,
中, ,
, ,
, ,则
,则
 或
或

 =25,且
=25,且 ,则
,则 .
. 与圆
与圆 相切,且与直线
相切,且与直线
 平行,则直线
平行,则直线 (
( 为自然对数的底数),则
为自然对数的底数),则 的值为 .
的值为 . 满足
满足 ,
, .
. 满足
满足 ,求数列
,求数列
 ;
; 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号