2022年甘肃省兰州市中考数学试卷
下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
无色酚酞溶液是一种常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色.现有 瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )
| A. |
|
B. |
|
C. |
|
D. |
|
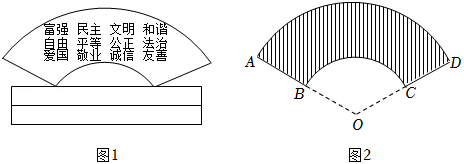
如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以 为圆心, 长分别为半径,圆心角 形成的扇面,若 ,则阴影部分的面积为( )
| A. |
|
B. |
|
C. |
|
D. |
|
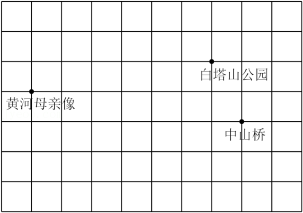
如图,小刚在兰州市平面地图的部分区域建立了平面直角坐标系,如果白塔山公园的坐标是 ,中山桥的坐标是 ,那么黄河母亲像的坐标是________.
2022年3月12日是我国第44个植树节,某林业部门为了考察某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:
幼树移植数(棵) |
|
|
|
|
|
|
|
幼树移植成活数(棵) |
|
|
|
|
|
|
|
幼树移植成活的频率 |
|
|
|
|
|
|
|
估计该种幼树在此条件下移植成活的概率是_____.(结果精确到 )
如图,小睿为测量公园的一凉亭 的高度,他先在水平地面点 处用高 的测角仪DE测得 ,然后沿 方向向前走 到达点 处,在点 处用高 的测角仪 测得 .求凉亭 的高度.( 三点共线, .结果精确到 )

(参考数据: )
人口问题是“国之大者”,以习近平同志为核心的党中央高度重视人口问题,准确把握人口发展形势,有利于推动社会持续健康发展,为开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军创造良好的条件.某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:
信息一:普查登记的全国大陆 个省、自治区、直辖市人口数的频数分布直方图如下:
(数据分成 组: )

信息二:普查登记的全国大陆 个省、自治区、直辖市人口数(百万人)在 这一组的数据是: ;
信息三: 年全国大陆人口数及自然增长率;

请根据以上信息,解答下列问题:
(1)普查登记的全国大陆 个省、自治区、直辖市人口数的中位数为 ____百万人.
(2)下列结论正确的是____.(只填序号)
①全国大陆 个省、自治区、直辖市中人口数大于等于 (百万人)的有2个地区;
②相对于 年, 年全国大陆人口自然增长率降低,全国大陆人口增长缓慢;
③ 年全国大陆人口自然增长率持续降低.
(3)请写出 年全国大陆人口数、全国大陆人口自然增长率的变化趋势,结合变化趋势谈谈自己的看法.
综合与实践
问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎(wèi)范、芯组成的铸型(如图1),它的端面是圆形.如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记 三点;将“矩”向右旋转,使它左侧边落在 点上,“矩”的另一条边与的交点标记为 点,这样就用“矩”确定了圆上等距离的 四点,连接 相交于点 ,即 为圆心.

问题解决:(1)请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心 .如图3,点 在 上, ,且 ,请作出圆心 .(保留作图痕迹,不写作法)
类比迁移:(2)小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果 和 不相等,用三角板也可以确定圆心 .如图4,点 在 上, ,请作出圆心 .(保留作图痕迹,不写作法)
拓展探究:(3)小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点 是 上任意三点,请用不带刻度的直尺和圆规作出圆心 .(保留作图痕迹,不写作法)请写出你确定圆心的理由:________________.

如图,在 中, , 为 边上一动点, ,垂足为 .设 两点间的距离为 , 两点间的距离为 (当点 和 点重合时, 两点间的距离为 ).
小明根据学习函数的经验,对因变量 随自变量 的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
(1)列表:下表的已知数据是根据 两点间的距离 进行取点、画图、测量,分别得到了 与 的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请你通过计算,补全表格: _____;
(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点 ,并画出函数 关于 的图象;

(3)探究性质:随着自变量 的不断增大,函数 的变化趋势:__________;
(4)解决问题:当 时, 的长度大约是_____ .(结果保留两位小数)

掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投实心球,实心球行进路线是一条抛物线,行进高度 与水平距离 之间的函数关系如图2所示,掷出时起点处高度为 ,当水平距离为 时,实心球行进至最高点 处.
(1)求 关于 的函数表达式;
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于 ,此项考试得分为满分 分.该女生在此项考试中是否得满分,请说明理由.

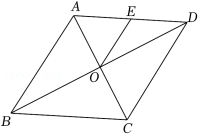
如图,点A在反比例函数 的图象上, 轴,垂足为 ,过 作 轴,交过 点的一次函数 的图象于D点,交反比例函数的图象于 点, .
(1)求反比例函数 和一次函数 的表达式;
(2)求 的长.

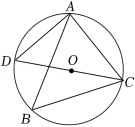
如图, 是 的外接圆, 是直径, ,连接 , , 与 相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点 的“倾斜系数” .
(1)求点 的“倾斜系数” 的值;
(2)①若点 的“倾斜系数” ,请写出 和 的数量关系,并说明理由;
②若点 的“倾斜系数” ,且 ,求 的长;
(3)如图,边长为 的正方形 沿直线 运动, 是正方形 上任意一点,且点 的“倾斜系数” ,请直接写出 的取值范围.

综合与实践
【问题情境】
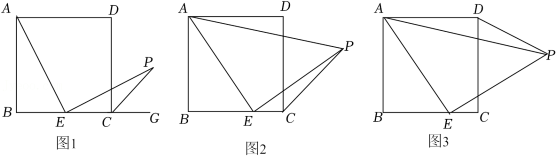
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号