综合与实践
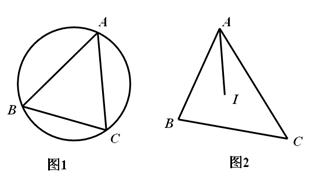
问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎(wèi)范、芯组成的铸型(如图1),它的端面是圆形.如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记 三点;将“矩”向右旋转,使它左侧边落在 点上,“矩”的另一条边与的交点标记为 点,这样就用“矩”确定了圆上等距离的 四点,连接 相交于点 ,即 为圆心.

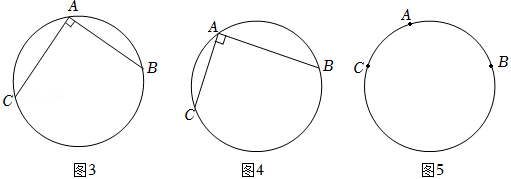
问题解决:(1)请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心 .如图3,点 在 上, ,且 ,请作出圆心 .(保留作图痕迹,不写作法)
类比迁移:(2)小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果 和 不相等,用三角板也可以确定圆心 .如图4,点 在 上, ,请作出圆心 .(保留作图痕迹,不写作法)
拓展探究:(3)小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点 是 上任意三点,请用不带刻度的直尺和圆规作出圆心 .(保留作图痕迹,不写作法)请写出你确定圆心的理由:________________.
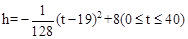 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?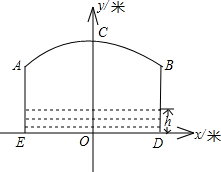

 粤公网安备 44130202000953号
粤公网安备 44130202000953号