2020年贵州省黔南州中考数学试卷

3的相反数是（　　）

A．﹣3B．3C． $-\frac{1}{3}$D． $\frac{1}{3}$

观察下列图形，是中心对称图形的是（　　）

A．B．

C．D．

某市2020年参加中考的考生人数的为93400人，将93400用科学记数法表示为（　　）

A． $934\times {10}^2$B． $93.4\times {10}^3$C． $9.34\times {10}^4$D． $0.934\times {10}^5$

下列四个几何体中，左视图为圆的是（　　）

A．B．C．D．

下列运算正确的是（　　）

A． $（a^3{）}^4＝a^{12}$B． $a^3•a^4＝a^{12}$C． $a^2+a^2＝a^4$D． $（\mathit{ab}{）}^2＝a{b}^2$

如图，将矩形纸条 $\mathit{ABCD}$折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E与BF交于点G．已知 $\angle \mathit{BGD}\text{'}＝30°$，则 $\angle \alpha$的度数是（　　）

A． $30°$B． $45°$C． $74°$D． $75°$

如图，数学活动小组利用测角仪和皮尺测量学校旗杆的高度，在点D处测得旗杆顶端A的仰角 $\angle \mathit{ADE}为55°$，测角仪CD的高度为1米，其底端C与旗杆底端B之间的距离为6米，设旗杆AB的高度为x米，则下列关系式正确的是（　　）

A． $\mathit{tan}55°=\frac{6}{x-1}$B． $\mathit{tan}55°=\frac{x-1}{6}$

C． $\sin 55°=\frac{x-1}{6}$D． $\cos 55°=\frac{x-1}{6}$

某超市正在热销一种商品，其标价为每件12元，打8折销售后每件可获利2元，该商品每件的进价为（　　）

A．7.4元B．7.5元C．7.6元D．7.7元

已知等腰三角形的一边长等于4，一边长等于9，则它的周长为（　　）

A．9B．17或22C．17D．22

已知 $a=\sqrt{17}-1$，a介于两个连续自然数之间，则下列结论正确的是（　　）

A． $1＜a＜2$B． $2＜a＜3$C． $3＜a＜4$D． $4＜a＜5$

分解因式： $a^3﹣2a^{2}b+a{b}^2＝$　      　．

若单项式 $a^m{}^{﹣2}{b}^n{}^{+7}$与单项式 $﹣3a^4{b}^4$的和仍是一个单项式，则 $m﹣n＝$　 　．

若一组数据2，3，x，1，5，7的众数为7，则这组数据的中位数为　　．

函数 $y＝x﹣1$的图象一定不经过第　 　象限．

如图，在平面直角坐标系中，直线 $y=-\frac{4}{3}x+4$与x轴、y轴分别交于A、B两点，点C在第二象限，若 $\mathit{BC}＝\mathit{OC}＝\mathit{OA}$，则点C的坐标为　    　．

如图所示，在四边形 $\mathit{ABCD}$中， $\angle B＝90°$， $\mathit{AB}＝2$， $\mathit{CD}＝8$．连接AC， $\mathit{AC}\perp \mathit{CD}$，若 $\mathit{sin}\angle \mathit{ACB}=\frac{\mathit{AB}}{\mathit{AC}}=\frac{1}{3}$，则AD长度是　 　．

已知菱形的周长为 $4\sqrt{5}$，两条对角线长的和为6，则菱形的面积为　 　．

如图，正方形 $\mathit{ABCD}$的边长为10，点A的坐标为 $\mathit{（﹣}8，0）$，点B在y轴上，若反比例函数 $y=\frac{k}{x}（k\ne 0）$的图象过点C，则该反比例函数的解析式为　 　．

《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”

译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问每头牛、每只羊各值金多少两？”

设每头牛值金x两，每只羊值金y两，可列方程组为 　             ．

对于实数a，b，定义运算“ $a*b=\left\{\begin{array}{c}a2-\mathit{ab}\left(a＞b\right)\\ \mathit{ab}-b2\left(a\le b\right)\end{array}\right.$”例如 $4*2$，因为 $4＞2$，所以 $4*2＝4^2﹣4\times 2＝8$．若 $x_1，x_2$是一元二次方程 $x^2﹣8x+16＝0$的两个根，则 $x_1*x_2=$　　．

（1）计算 ${(-\frac{1}{2})}^{-1}-3\tan 60°+\left|-\sqrt{3}\right|+{(2\cos 60°-2020)}^0$；

（2）解不等式组： $\left\{\begin{array}{c}\frac{3-x}{2}\le 1\\ 3x+2\ge 4\end{array}\right.$．

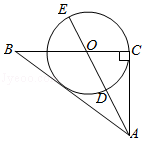
古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的圆”，请研究如下美丽的圆，如图， $\mathit{Rt}△\mathit{ABC}$中， $\angle \mathit{BCA}＝90°$， $\mathit{AC}＝3$， $\mathit{BC}＝4$，点O在线段 $\mathit{BC}$上，且 $\mathit{OC}=\frac{3}{2}$，以O为圆心． $\mathit{OC}$为半径的 $\odot O$交线段AO于点D，交线段AO的延长线于点E．

（1）求证： $\mathit{AB}$是 $\odot O$的切线；

（2）研究过短中，小明同学发现 $\frac{\mathit{AC}}{\mathit{AE}}=\frac{\mathit{AD}}{\mathit{AC}}$，回答小明同学发现的结论是否正确？如果正确，给出证明；如果不正确，说明理由．

勤劳是中华民族的传统美德，学校要求学们在家帮助父母做一些力所能及的家务．在学期初，小丽同学随机调查了七年级部分同学寒假在家做家务的总时间，设被调查的每位同学寒假在家做家务的总时间为x小时，将做家务的总时间分为五个类别： $A（0\le x＜10）$， $B（10\le x＜20）$， $C（20\le x＜30）$， $D（30\le x＜40）$， $E（x\ge 40）$．并将调查结果绘制了如图两幅不完整的统计图：

根据统计图提供的作息，解答下列问题：

（1）本次共调查了　　名学生；

（2）根据以上信息直接在答题卡上补全条形统计图；

（3）扇形統计图中m＝　　，类别D所对应的扇形圆心角α的度数是　　度；

（4）若该校七年级共有400名学生，根据抽样调查的结果，估计该校七年級有多少名学生寒假在家做家务的总时间不低于20小时？

某单位计划购买甲、乙两种品牌的消毒剂，乙种品牌消毒剂每瓶的价格比甲种品牌消毒剂每瓶价格的3倍少50元，已知用300元购买甲种品牌消毒剂的数量与用400元购买乙种品牌消毒剂的数量相同．

（1）求甲、乙两种品牌消毒剂每瓶的价格各是多少元？

（2）若该单位从超市一次性购买甲、乙两种品牌的消毒剂共40瓶，且总费用为1400元，求购买了多少瓶乙种品牌消毒剂？

在2020年新冠肺炎疫情期间，某中学响应政府有“停课不停学”的号召，充分利用网络资源进行网上学习，九年级1班的全体同学在自主完成学习任务的同时，彼此关怀，全班每两个同学都通过一次电话，互相勉励，共同提高，如果该班共有48名同学，若每两名同学之间仅通过一次电话，那么全班同学共通过多少次电话呢？我们可以用下面的方式来解决问题．

用点A₁、A₂、A₃…A₄₈分表示第1名同学、第2名同学、第3名同学…第48名同学，把该班级人数x与通电话次数y之间的关系用如图模型表示：

（1）填写上图中第四个图中y的值为　　，第五个图中y的值为　　．

（2）通过探索发现，通电话次数y与该班级人数x之间的关系式为　 　，当 $x＝48$时，对应的y＝　   　．

（3）若九年级1班全体女生相互之间共通话190次，问：该班共有多少名女生？

如图，已知AB是⊙O的直径，⊙O经过 $\mathit{Rt}△\mathit{ACD}$的直角边DC上的点F，交AC边于点E，点F是弧EB的中点， $\angle C＝90°$，连接AF．

（1）求证：直线CD是⊙O切线．

（2）若 $\mathit{BD}＝2$， $\mathit{OB}＝4$，求 $\mathit{tan}\angle \mathit{AFC}$的值．

如图（1），在平面直角坐标系中，抛物线 $y＝a{x}^2+\mathit{bx}+4（a\ne 0）$与y轴交于点A，与x轴交于点 $C\mathit{（﹣}2，0）$，且经过点B（8，4），连接AB，BO，作 $\mathit{AM}\perp \mathit{OB}$于点M，将 $\mathit{Rt}△\mathit{OMA}$沿y轴翻折，点M的对应点为点N．解答下列问题：

（1）抛物线的解析式为　            ，顶点坐标为　           ；

（2）判断点N是否在直线AC上，并说明理由；

（3）如图（2），将图（1）中 $\mathit{Rt}△\mathit{OMA}$沿着OB平移后，得到 $\mathit{Rt}△\mathit{DEF}$．若DE边在线段OB上，点F在抛物线上，连接AF，求四边形 $\mathit{AMEF}$的面积．