2020年山东省威海市中考数学试卷
人民日报讯,2020年6月23日,中国成功发射北斗系统第55颗导航卫星.至此中国提前半年全面完成北斗三号全球卫星导航系统星座部署.北斗三号卫星上配置的新一代国产原子钟,使北斗导航系统授时精度达到了十亿分之一秒.十亿分之一用科学记数法可以表示为
A. B. C. D.
为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对初二级部学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是

A.本次调查的样本容量是600
B.选“责任”的有120人
C.扇形统计图中“生命”所对应的扇形圆心角度数为
D.选“感恩”的人数最多
如图,点 ,点 都在反比例函数 的图象上.过点 分别向 轴、 轴作垂线,垂足分别为点 , .连接 , , .若四边形 的面积记作 , 的面积记作 ,则

A. B. C. D.
七巧板是大家熟悉的一种益智玩具.用七巧板能拼出许多有趣的图案.小李将一块等腰直角三角形硬纸板(如图① 切割七块,正好制成一副七巧板(如图② .已知 ,则图中阴影部分的面积为
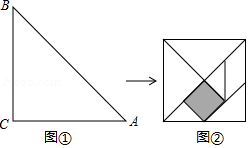
A. B. C. D.
如图,抛物线 交 轴于点 , ,交 轴于点 .若点 坐标为 ,对称轴为直线 ,则下列结论错误的是

A.二次函数的最大值为 B.
C. D.
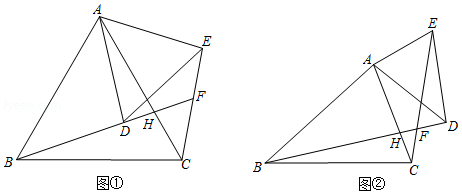
如图,在 中,对角线 , , , 为 的中点, 为边 上一点,直线 交 于点 ,连结 , .下列结论不成立的是
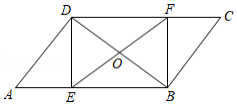
A.四边形 为平行四边形
B.若 ,则四边形 为矩形
C.若 ,则四边形 为菱形
D.若 ,则四边形 为正方形
如图,四边形 是一张正方形纸片,其面积为 .分别在边 , , , 上顺次截取 ,连接 , , , .分别以 , , , 为轴将纸片向内翻折,得到四边形 .若四边形 的面积为 ,则 .

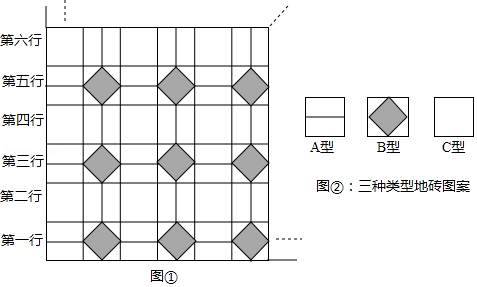
如图①,某广场地面是用 , , 三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块 型)地砖记作 ,第二块 型)地砖记作 若 位置恰好为 型地砖,则正整数 , 须满足的条件是 .
在“旅游示范公路”建设的过程中,工程队计划在海边某路段修建一条长 的步行道.由于采用新的施工方式,平均每天修建步行道的长度是计划的1.5倍,结果提前5天完成任务.求计划平均每天修建步行道的长度.
居家学习期间,小晴同学运用所学知识在自家阳台测对面大楼的高度.如图,她利用自制的测角仪测得该大楼顶部的仰角为 ,底部的俯角为 ;又用绳子测得测角仪距地面的高度 为 .求该大楼的高度(结果精确到 .
(参考数据: , ,

如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

小伟和小梅两位同学玩掷骰子的游戏,两人各掷一次均匀的骰子.以掷出的点数之差的绝对值判断输赢.若所得数值等于0,1,2,则小伟胜;若所得数值等于3,4,5,则小梅胜.
(1)请利用表格分别求出小伟、小梅获胜的概率;
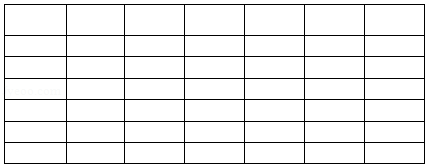
(2)判断上述游戏是否公平.如果公平,请说明理由;如果不公平,请利用表格修改游戏规则,以确保游戏的公平性.
已知,在平面直角坐标系中,抛物线 的顶点为 .点 的坐标为 .
(1)求抛物线过点 时顶点 的坐标;
(2)点 的坐标记为 ,求 与 的函数表达式;
(3)已知 点的坐标为 ,当 取何值时,抛物线 与线段 只有一个交点.
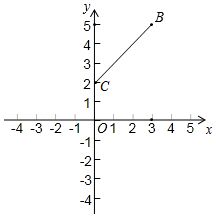




 B.
B.
 D.
D.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号