2018年江苏省苏州市中考数学试卷
如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是
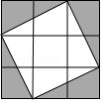
A. B. C. D.
如图,某海监船以20海里 小时的速度在某海域执行巡航任务,当海监船由西向东航行至 处时,测得岛屿 恰好在其正北方向,继续向东航行1小时到达 处,测得岛屿 在其北偏西 方向,保持航向不变又航行2小时到达 处,此时海监船与岛屿 之间的距离(即 的长)为

A.40海里B.60海里C. 海里D. 海里
如图,在 中,延长 至 ,使得 ,过 中点 作 (点 位于点 右侧),且 ,连接 .若 ,则 的长为

A.3B.4C. D.
如图,矩形 的顶点 , 在 轴的正半轴上,反比例函数 在第一象限内的图象经过点 ,交 于点 .若 , , ,则 的值为

A.3B. C.6D.12
如图, 是一块直角三角板, , ,现将三角板叠放在一把直尺上,使得点 落在直尺的一边上, 与直尺的另一边交于点 , 与直尺的两边分别交于点 , .若 ,则 的度数为 .

如图, 的正方形网格纸上有扇形 和扇形 ,点 , , , , 均在格点上.若用扇形 围成一个圆锥的侧面,记这个圆锥的底面半径为 ;若用扇形 围成另一个圆锥的侧面,记这个圆锥的底面半径为 ,则 的值为 .

如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为 (结果留根号).

如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:

(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有600名学生,试估计该校选择“足球”项目的学生有多少人?
某学校准备购买若干台 型电脑和 型打印机.如果购买1台 型电脑,2台 型打印机,一共需要花费5900元;如果购买2台 型电脑,2台 型打印机,一共需要花费9400元.
(1)求每台 型电脑和每台 型打印机的价格分别是多少元?
(2)如果学校购买 型电脑和 型打印机的预算费用不超过20000元,并且购买 型打印机的台数要比购买 型电脑的台数多1台,那么该学校至多能购买多少台 型打印机?
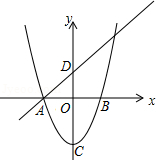
如图,已知抛物线 与 轴交于点 , (点 位于点 的左侧), 为顶点,直线 经过点 ,与 轴交于点 .
(1)求线段 的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为 .若新抛物线经过点 ,并且新抛物线的顶点和原抛物线的顶点的连线 平行于直线 ,求新抛物线对应的函数表达式.
如图, 是 的直径,点 在 上, 垂直于过点 的切线,垂足为 , 垂直 ,垂足为 .延长 交 于点 ,连接 , 与 相交于点 ,连接 .
(1)求证: ;
(2)若 ,求证: 是等腰直角三角形.

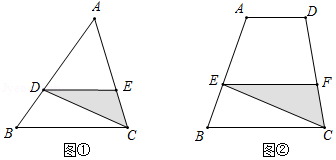
问题1:如图①,在 中, , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 的面积为 , 的面积为 .
(1)当 时, ;
(2)设 ,请你用含字母 的代数式表示 .
问题2:如图②,在四边形 中, , , , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 ,四边形 的面积为 , 的面积为 .请你利用问题1的解法或结论,用含字母 的代数式表示 .
 B.
B.
 D.
D.
 B.
B.
 D.
D.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号