2018年浙江省杭州市中考数学试卷
测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是
A.方差B.标准差C.中位数D.平均数
某次知识竞赛共有20道题,规定:每答对一道题得 分,每答错一道题得 分,不答的题得0分,已知圆圆这次竞赛得了60分,设圆圆答对了 道题,答错了 道题,则
A. B. C. D.
一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别标有数字 朝上一面的数字,任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于
A. B. C. D.
四位同学在研究函数 , 是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, ,已知这四位同学中只有一位发现的结论是错误的,则该同学是
A.甲B.乙C.丙D.丁
如图,在 中,点 在 边上, ,与边 交于点 ,连接 .记 , 的面积分别为 , ,

A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
某日上午,甲,乙两车先后从 地出发沿同一条公路匀速前往 地,甲车8点出发,如图是其行驶路程 (千米)随行驶时间 (小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度 (单位:千米 小时)的范围是 .

折叠矩形纸片 时,发现可以进行如下操作:①把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上;②把纸片展开并铺平;③把 翻折,点 落在线段 上的点 处,折痕为 ,点 在 边上,若 , ,则 .

已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货.设平均卸货速度为 (单位:吨 小时),卸完这批货物所需的时间为 (单位:小时).
(1)求 关于 的函数表达式.
(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量的频数表
组别 |
频数 |
|
2 |
|
|
|
3 |
|
1 |
(1)求 的值;
(2)已知收集的可回收垃圾以0.8元 被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到50元?

设一次函数 , 是常数, 的图象过 , 两点.
(1)求该一次函数的表达式;
(2)若点 在该一次函数图象上,求 的值.
(3)已知点 , 和点 , 在该一次函数图象上,设 ,判断反比例函数 的图象所在的象限,说明理由.
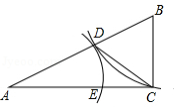
如图,在 中, ,以点 为圆心, 长为半径画弧,交线段 于点 ;以点 为圆心, 长为半径画弧,交线段 于点 ,连接 .
(1)若 ,求 的度数.
(2)设 , .
①线段 的长是方程 的一个根吗?说明理由.
②若 ,求 的值.
设二次函数 , 是常数, .
(1)判断该二次函数图象与 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 , , 三个点中的其中两个点,求该二次函数的表达式.
(3)若 ,点 , 在该二次函数图象上,求证: .



 粤公网安备 44130202000953号
粤公网安备 44130202000953号