2018年四川省凉山州中考数学试卷
如图,数轴上点 对应的数为2, 于 ,且 ,以 为圆心, 长为半径作弧,交数轴于点 ,则 长为
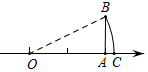
A.3B. C. D.
如图,在 中,按以下步骤作图:①分别以 、 为圆心,大于 长为半径作弧,两弧相交于 、 两点;②作直线 交 于 ,连接 .若 , ,则

A. B. C. D.
凉山州某校举行“禁毒防艾”知识竞赛,该校八年级(1)班答题情况如图所示,则该班正确答题数所组成的一组数据的众数和中位数分别是

A.14、15B.14、20C.20、15D.20、16
下列说法正确的是
①平行四边形既是中心对称图形,又是轴对称图形;②同一物体的三视图中,俯视图与左视图的宽相等;③线段的正投影是一条线段;④主视图是正三角形的圆锥的侧面展开图一定是半圆;⑤图形平移的方向总是水平的,图形旋转后的效果总是不同的.
A.①③B.②④C.③⑤D.②⑤
无人机在 处测得正前方河流两岸 、 的俯角分别为 、 ,此时无人机的高度是 ,则河流的宽度 为

A. B.
C. D.
方程 中,系数 、 可以在1、2、3、4中任取一值 、 可以取相同的值),则 、 所取的值使方程 有实数根的概率是 .
在 中, 、 分别是 、 上的点,将平行四边形 沿 所在直线翻折,使点 与点 重合,且点 落在点 处.
(1)求证:△ ;
(2)连接 ,若 , ,求四边形 的面积.

西昌市教科知局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查(被调查学生每人只能选一项),并将抽样调查的数据绘制成图1、图2两幅统计图,根据统计图提供的信息解答下列问题:
(1) 年抽取的调查人数最少; 年抽取的调查人数中男生、女生人数相等;
(2)求图2中“短跑”在扇形图中所占的圆心角 的度数;
(3)2017年抽取的学生中,喜欢羽毛球和短跑的学生共有多少人?
(4)如果2017年全市共有3.4万名中学生,请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人?

在平面直角坐标系中的位置如图所示,直线 与双曲线 在第一象限的图象相交于 、 两点,且 , 是 的中点.
(1)连接 ,若 的面积为 , 的面积为 ,则 (直接填“ ”“ ”或“ ” ;
(2)求 和 的解析式;
(3)请直接写出当 取何值时 .

在平面直角坐标系中的位置如图所示, ,将 绕 点,逆时针旋转 得到△ , ,交 轴于 ,若△ △ ,则点 的坐标 .

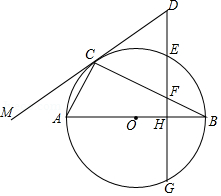
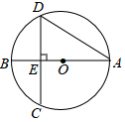
已知: 内接于 , 是 的直径,作 于 ,交 于 ,延长 交直线 于 ,且 ,求证:
(1) 是 的切线;
(2) 是等腰三角形.
阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数 、 的算术平均数, 叫做正数 、 的几何平均数,它是解决最大(小 值问题的有力工具.
例如:在 的条件下,当 为何值时, 有最小值,最小值是多少?
解: , 即是
当且仅当 即 时, 有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若 ,函数 ,当 为何值时,函数有最值,并求出其最值.
(2)当 时,式子 成立吗?请说明理由.
结合西昌市创建文明城市要求,某小区业主委员会决定把一块长 ,宽 的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于 ,不大于 ,预计活动区造价60元 ,绿化区造价50元 ,设绿化区域较长直角边为 .
(1)用含 的代数式表示出口的宽度;
(2)求工程总造价 与 的函数关系式,并直接写出 的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出 为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化 ,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少 .




 粤公网安备 44130202000953号
粤公网安备 44130202000953号