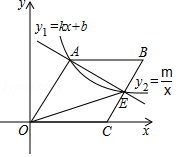
在平面直角坐标系中的位置如图所示,直线 与双曲线 在第一象限的图象相交于 、 两点,且 , 是 的中点.
(1)连接 ,若 的面积为 , 的面积为 ,则 (直接填“ ”“ ”或“ ” ;
(2)求 和 的解析式;
(3)请直接写出当 取何值时 .
相关知识点
推荐套卷
在平面直角坐标系中的位置如图所示,直线 与双曲线 在第一象限的图象相交于 、 两点,且 , 是 的中点.
(1)连接 ,若 的面积为 , 的面积为 ,则 (直接填“ ”“ ”或“ ” ;
(2)求 和 的解析式;
(3)请直接写出当 取何值时 .
