2016年江苏省连云港市中考数学试卷
据市统计局调查数据显示,我市目前常住人口约为4470000人,数据“4470000”用科学记数法可表示为
A. B. C. D.
姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:在每一个象限内, 值随 值的增大而减小.根据他们的描述,姜老师给出的这个函数表达式可能是
A. B. C. D.
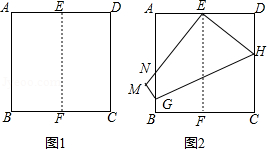
如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为 、 、 ;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为 、 、 .其中 , , , ,则

A.86B.64C.54D.48
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以 为圆心, 为半径画圆,选取的格点中除点 外恰好有3个在圆内,则 的取值范围为
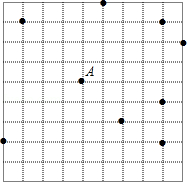
A. B. C. D.
在新年晚会的投飞镖游戏环节中,7名同学的投掷成绩(单位:环)分别是:7,9,9,4,9,8,8,则这组数据的众数是 .
如图1,将正方形纸片 对折,使 与 重合,折痕为 .如图2,展开后再折叠一次,使点 与点 重合,折痕为 ,点 的对应点为点 , 交 于 .若 ,则 .
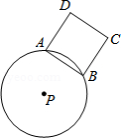
如图, 的半径为5, 、 是圆上任意两点,且 ,以 为边作正方形 (点 、 在直线 两侧).若 边绕点 旋转一周,则 边扫过的面积为 .
某自行车公司调查阳光中学学生对其产品的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为 、 、 、 .根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中 .
(2)请根据数据信息补全条形统计图.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的 .环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度 与时间 (天 的变化规律如图所示,其中线段 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度 与时间 成反比例关系.
(1)求整改过程中硫化物的浓度 与时间 的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的 ?为什么?

如图,在平面直角坐标系 中,抛物线 经过两点 , .过点 作 轴,交抛物线于点 ,交 轴于点 .
(1)求此抛物线对应的函数表达式及点 的坐标;
(2)若抛物线上存在点 ,使得 的面积为 ,求出点 的坐标;
(3)连接 、 、 、 ,在坐标平面内,求使得 与 相似(边 与边 对应)的点 的坐标.

我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图, 为入射光线,入射点为 , 为法线(过入射点 且垂直于镜面的直线), 为反射光线,此时反射角 等于入射角 .
问题思考:
(1)如图1,一束光线从点 处入射到平面镜上,反射后恰好过点 ,请在图中确定平面镜上的入射点 ,保留作图痕迹,并简要说明理由;
(2)如图2,两平面镜 、 相交于点 ,且 ,一束光线从点 出发,经过平面镜反射后,恰好经过点 .小昕说,光线可以只经过平面镜 反射后过点 ,也可以只经过平面镜 反射后过点 .除了小昕的两种做法外,你还有其它做法吗?如果有,请在图中画出光线的行进路线,保留作图痕迹,并简要说明理由;

问题拓展:
(3)如图3,两平面镜 、 相交于点 ,且 ,一束光线从点 出发,且平行于平面镜 ,第一次在点 处反射,经过若干次反射后又回到了点 ,如果 和 的长均为 ,求这束光线经过的路程;
(4)如图4,两平面镜 、 相交于点 ,且 ,一束光线从点 出发,经过若干次反射后,最后反射出去时,光线平行于平面镜 .设光线出发时与射线 的夹角为 ,请直接写出满足条件的所有 的度数(注 、 足够长)







 粤公网安备 44130202000953号
粤公网安备 44130202000953号