2018年内蒙古巴彦淖尔市中考数学试卷

$\sqrt{\text{16}}$ 的算术平方根的倒数是（　　）

下列运算正确的是（　　）

下列四个汽车图标中，既是轴对称图形又是中心对称图形的图标是（　　）

若关于 x， y的方程组 $\left\{\begin{array}{c}\text{2}x+y=4\\ x+2y=-3m+2\end{array}\right.$ 的解满足 x﹣ y＞﹣ $\frac{3}{2}$ ，则 m的最小整数解为（　　）

如图是一个几何体的三视图，则这个几何体的表面积是（　　）

如图，△ ABC是一块绿化带，将阴影部分修建为花圃，已知 AB＝13， AC＝5， BC＝12，阴影部分是△ ABC的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（　　）

小敏上月在某文具店正好用30元钱买了几本笔记本，本月再去买时，恰遇此文具店搞优惠酬宾活动，同样的笔记本，每本比上月便宜1元，结果小敏只比上次多用了6元钱，却比上次多买了8本，若设她上月买了 x本笔记本，则根据题意可列方程为（　　）

南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至 B处时，测得该岛位于正北方向10（1+ $\sqrt{3}$ ）海里的 C处，为了防止某国海巡警干扰，请求我 A处的渔监船前往 C处护航．如图，已知 C位于 A处的东北方向上， A位于 B的北偏西30°方向上，则 A和 C之间的距离为（　　）

如图，在扇形 AOB中，∠ AOB＝90°，点 C为 OA的中点， CE⊥ OA交 $\stackrel{⏜}{\mathit{AB}}$ 于点 E，以点 O为圆心， OC的长为半径作 $\stackrel{⏜}{\mathit{CD}}$ 交 OB于点 D．若 OA＝4，则图中阴影部分的面积为（　　）

如图是本地区一种产品30天的销售图象，图①是产品日销售量 y（单位：件）与时间 t（单位：天）的函数关系，图②是一件产品的销售利润 z（单位：元）与时间 t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润．下列结论错误的是（　　）

分解因式：8 a ²﹣8 a ³﹣2 a＝ 　 　．

如图，将平行四边形 ABCD沿对角线 BD折叠，使点 A落在点 A′处，∠1＝∠2＝48°，则∠ A′的度数为 　 　．

如图，菱形 ABCD的面积为120 cm ²，正方形 AECF的面积为72 cm ²，则菱形的边长为 　　．（结果中如有根号保留根号）

两组数据 m， n，6与1， m，2 n，7的平均数都是6，若将这两组数据合并成一组数据，则这组新数据的方差是 　　．

如图，正三角形 ABO的边长为2， O为坐标原点，点 A在 x轴上，点 B在第二象限，△ ABO沿 x轴正方向做无滑动的翻滚，经一次翻滚后得△ A ₁ B ₁ O，则翻滚三次后点 B的对应点的坐标是 　　，翻滚90次后 AB的中点 M经过的路径长为 　　．

如图，⊙ O为等腰三角形 ABC的外接圆， AB是⊙ O的直径， AB＝12， P为 $\stackrel{⏜}{\mathit{BC}}$ 上任意一点（不与点 B， C重合），直线 CP交 AB的延长线于点 Q，⊙ O在点 P处的切线 PD交 BQ于点 D，则下列结论：①若∠ PAB＝30°，则 $\stackrel{⏜}{\mathit{PB}}$ 的长为π；②若 PD∥ BC，则 AP平分∠ CAB；③若 PB＝ BD，则 PD＝6 $\sqrt{3}$ ；④无论点 P在 $\stackrel{⏜}{\mathit{BC}}$ 上的位置如何变化， CP• CQ＝108．其中正确结论的序号为 　　．

（1）计算： ${(-1)}^{2018}-2\cos {30}^{\circ }-{\left(\frac{1}{2}\right)}^{-2}-|\sqrt{3}-2|+{(2018-\pi )}^0$

（2）先化简，再求值： $\left(\frac{x^2-2x+1}{x^2-x}-\frac{4-x^2}{x^2+2x}\right)÷\frac{x-4}{x}$ ，且 x为满足﹣3＜ x＜2的整数．

工人师傅用一块长为12分米，宽为8分米的矩形铁皮制作一个无盖长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

（1）请在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求当长方体底面面积为32平方分米时，裁掉的正方形边长是多少？

（2）若要求制作的长方体的底面长不大于底面宽的5倍（长大于宽），并将容器外表面进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，求裁掉的正方形边长为多少时，总费用最低，最低费用为多少元？

某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额（单位：万元），并根据统计的这组销售额数据，绘制出如下的统计图1和图2，请根据相关信息，解答下列问题：

（1）该商场服装部营业员的人数为 　　，图1中 m的值为 　　；

（2）求统计的这组销售额数据的平均数、众数和中位数．

小美周末来到公园，发现在公园一角有一种"守株待兔"游戏．游戏设计者提供了一只兔子和一个有 A， B， C， D， E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定：①玩家只能将小兔从 A， B两个出入口放入：②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值4元的小兔玩具，否则应付费3元．

（1）请用画树状图的方法，列举出该游戏的所有可能情况；

（2）小美得到小兔玩具的机会有多大？

（3）假设有125人次玩此游戏，估计游戏设计者可赚多少元．

如图，在平行四边形 ABCD中， E， F分别是 AB， BC边上的中点， CE⊥ AB，垂足为 E， AF⊥ BC，垂足为 F， AF与 CE相交于点 G；

（1）求证：△ CFG≌△ AEG；

（2）若 AB＝6，求四边形 AGCD的对角线 GD的长．

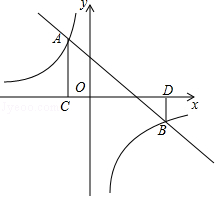
如图，直线 y＝﹣ x+2与反比例函数 y＝ $\frac{k}{x}$ （ k≠0）的图象交于 A（ a，3）， B（3， b）两点，过点 A作 AC⊥ x轴于点 C，过点 B作 BD⊥ x轴于点 D．

（1）求 a， b的值及反比例函数的解析式；

（2）若点 P在直线 y＝﹣ x+2上，且 S _{△ ACP}＝ S _{△ BDP}，请求出此时点 P的坐标；

（3）在 x轴正半轴上是否存在点 M，使得△ MAB为等腰三角形？若存在，请直接写出 M点的坐标；若不存在，说明理由．

如图， AB为⊙ O的直径， C， G是⊙ O上两点，过点 C的直线 CD⊥ BG于点 D，交 BA的延长线于点 E，连接 BC，交 OD于点 F，且 BC平分∠ ABD．

（1）求证： CD是⊙ O的切线；

（2）若 $\frac{\mathit{OF}}{\mathit{FD}}=\frac{2}{3}$ ，求∠ E的度数；

（3）连结 AD，在（2）的条件下，若 CD＝2 $\sqrt{3}$ ，求 AD的长．

如图，抛物线 y＝ ax ²+ bx+2与 x轴相交于 A（﹣1，0）， B（4，0）两点，与 y轴相交于点 C．

（1）求抛物线的解析式；

（2）将△ ABC绕 AB中点 M旋转180°，得到△ BAD．

①求点 D的坐标；

②判断四边形 ADBC的形状，并说明理由；

（3）在该抛物线对称轴上是否存在点 P，使△ BMP与△ BAD相似？若存在，请求出所有满足条件的 P点的坐标；若不存在，请说明理由．