2019年浙江省温州市中考数学试卷
太阳距离银河系中心约为250 000 000 000 000 000公里,其中数据250 000 000 000 000 000用科学记数法表示为
| A. |
|
B. |
|
C. |
|
D. |
|
在同一副扑克牌中抽取2张"方块",3张"梅花",1张"红桃".将这6张牌背面朝上,从中任意抽取1张,是"红桃"的概率为
| A. |
|
B. |
|
C. |
|
D. |
|
对温州某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),绘制成如图所示统计图.已知选择鲳鱼的有40人,那么选择黄鱼的有

| A. |
20人 |
B. |
40人 |
C. |
60人 |
D. |
80人 |
验光师测得一组关于近视眼镜的度数 (度 与镜片焦距 (米 的对应数据如下表,根据表中数据,可得 关于 的函数表达式为
近视眼镜的度数 (度 |
200 |
250 |
400 |
500 |
1000 |
镜片焦距 (米 |
0.50 |
0.40 |
0.25 |
0.20 |
0.10 |
| A. |
|
B. |
|
C. |
|
D. |
|
已知二次函数 ,关于该函数在 的取值范围内,下列说法正确的是
| A. |
有最大值 ,有最小值 |
B. |
有最大值0,有最小值 |
| C. |
有最大值7,有最小值 |
D. |
有最大值7,有最小值 |
如图,在矩形 中, 为 中点,以 为边作正方形 ,边 交 于点 ,在边 上取点 使 ,作 交 于点 ,交 于点 ,欧几里得在《几何原本》中利用该图解释了 ,现以点 为圆心, 为半径作圆弧交线段 于点 ,连结 ,记 的面积为 ,图中阴影部分的面积为 .若点 , , 在同一直线上,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良” 分及以上)的学生有 人.

图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚分米,展开角,晾衣臂分米,晾衣臂支架分米,且分米.当时,点离地面的距离为 ;分米,当从水平状态旋转到(在延长线上)时,点绕点随之旋转至上的点处,则为 分米.

车间有20名工人,某一天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个 |
9 |
10 |
11 |
12 |
13 |
15 |
16 |
19 |
20 |
工人人数(人 |
1 |
1 |
6 |
4 |
2 |
2 |
2 |
1 |
1 |
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
如图,在的方格纸中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点,,,重合.
(1)在图1中画一个格点,使点,,分别落在边,,上,且.
(2)在图2中画一个格点四边形,使点,,,分别落在边,,,上,且.

如图,在平面直角坐标系中,二次函数的图象交轴于点,(点在点的左侧)
(1)求点,的坐标,并根据该函数图象写出时的取值范围.
(2)把点向上平移个单位得点.若点向左平移个单位,将与该二次函数图象上的点重合;若点向左平移个单位,将与该二次函数图象上的点重合.已知,,求,的值.

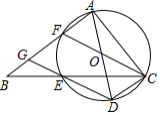
如图,在中,,点在边上,且,过,,三点的交于另一点,作直径,连结并延长交于点,连结,.
(1)求证:四边形是平行四边形.
(2)当,时,求的直径长.
某旅行团32人在景区游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区游玩.景区的门票价格为100元张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.









 粤公网安备 44130202000953号
粤公网安备 44130202000953号