2016年重庆市中考数学试卷(b卷)
据重庆商报2016年5月23日报道,第十九届中国(重庆)国际投资暨全球采购会(简称渝洽会)集中签约86个项目,投资总额1636亿元人民币,将数1636用科学记数法表示是
| A. |
|
B. |
|
C. |
|
D. |
|
下列调查中,最适合采用全面调查(普查)的是
| A. |
对重庆市居民日平均用水量的调查 |
| B. |
对一批 节能灯使用寿命的调查 |
| C. |
对重庆新闻频道"天天630"栏目收视率的调查 |
| D. |
对某校九年级(1)班同学的身高情况的调查 |
观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星, ,按此规律,图形⑧中星星的颗数是

| A. |
43 |
B. |
45 |
C. |
51 |
D. |
53 |
如图,在边长为6的菱形 中, ,以点 为圆心,菱形的高 为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积是

| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,某办公大楼正前方有一根高度是15米的旗杆 ,从办公楼顶端 测得旗杆顶端 的俯角 是 ,旗杆底端 到大楼前梯坎底边的距离 是20米,梯坎坡长 是12米,梯坎坡度 ,则大楼 的高度约为 (精确到0.1米,参考数据: , ,

| A. |
30.6 |
B. |
32.1 |
C. |
37.9 |
D. |
39.4 |
如果关于 的分式方程 有负分数解,且关于 的不等式组 的解集为 ,那么符合条件的所有整数 的积是
| A. |
|
B. |
0 |
C. |
3 |
D. |
9 |
点的坐标是,从,,0,1,2这五个数中任取一个数作为的值,再从余下的四个数中任取一个数作为的值,则点在平面直角坐标系中第二象限内的概率是 .
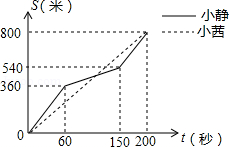
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程(米与所用的时间(秒之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 秒.
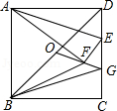
如图,在正方形中,,点在边上,,连接,将沿翻折,点落在点处,点是对角线的中点,连接并延长交于点,连接,,则的周长是 .
某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1600名学生每人都参加且只参加了其中一个社团的活动.校团委从这1600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:

参加本次调查有 名学生,根据调查数据分析,全校约有 名学生参加了音乐社团;请你补全条形统计图.
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的 , 两点,与 轴交于点 ,与 轴交于点 ,点 的坐标是 ,连接 , , .
(1)求反比例函数的解析式;
(2)连接 ,求 的面积.

近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了 .某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调 出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了 ,且储备猪肉的销量占总销量的 ,两种猪肉销售的总金额比5月20日提高了 ,求 的值.
我们知道,任意一个正整数 都可以进行这样的分解: , 是正整数,且 ,在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .例如12可以分解成 , 或 ,因为 ,所以 是12的最佳分解,所以 .
(1)如果一个正整数 是另外一个正整数 的平方,我们称正整数 是完全平方数.求证:对任意一个完全平方数 ,总有 ;
(2)如果一个两位正整数 , , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数 为"吉祥数",求所有"吉祥数"中 的最大值.
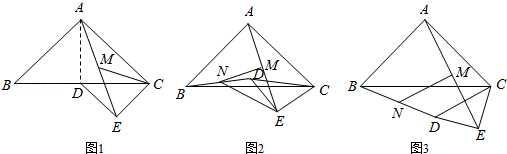
已知 是等腰直角三角形, , , , ,连接 ,点 是 的中点.
(1)如图1,若点 在 边上,连接 ,当 时,求 的长;
(2)如图2,若点 在 的内部,连接 ,点 是 中点,连接 , ,求证: ;
(3)如图3,将图2中的 绕点 逆时针旋转,使 ,连接 ,点 是 中点,连接 ,探索 的值并直接写出结果.
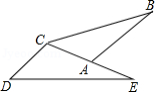
如图1,二次函数 的图象与一次函数 的图象交于 , 两点,点 的坐标为 ,点 在第一象限内,点 是二次函数图象的顶点,点 是一次函数 的图象与 轴的交点,过点 作 轴的垂线,垂足为 ,且 .
(1)求直线 和直线 的解析式;
(2)点 是线段 上一点,点 是线段 上一点, 轴,射线 与抛物线交于点 ,过点 作 轴于点 , 于点 .当 与 的乘积最大时,在线段 上找一点 (不与点 ,点 重合),使 的值最小,求点 的坐标和 的最小值;
(3)如图2,直线 上有一点 ,将二次函数 沿直线 平移,平移的距离是 ,平移后抛物线上点 ,点 的对应点分别为点 ,点 ;当△ 是直角三角形时,求 的值.







 粤公网安备 44130202000953号
粤公网安备 44130202000953号