2016年山西省中考数学试卷
以下问题不适合全面调查的是
| A. |
调查某班学生每周课前预习的时间 |
| B. |
调查某中学在职教师的身体健康状况 |
| C. |
调查全国中小学生课外阅读情况 |
| D. |
调查某校篮球队员的身高 |
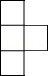
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是

| A. |
|
B. |
|
C. |
|
D. |
|
我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为

| A. |
千米 |
B. |
千米 |
C. |
千米 |
D. |
千米 |
甲、乙两个搬运工搬运某种货物,已知乙比甲每小时多搬运 ,甲搬运 所用时间与乙搬运 所用时间相等,求甲、乙两人每小时分别搬运多少 货物,设甲每小时搬运 货物,则可列方程为
| A. |
|
B. |
|
| C. |
|
D. |
|
将抛物线 向左平移 3 个单位, 再向上平移 5 个单位, 得到抛物线的函数表达式为
| A. |
A . B . C . D . |
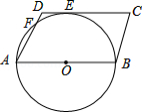
宽与长的比是 (约 的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 、 的中点 、 ,连接 :以点 为圆心,以 为半径画弧,交 的延长线于点 ;作 ,交 的延长线于点 ,则图中下列矩形是黄金矩形的是

| A. |
矩形 |
B. |
矩形 |
C. |
矩形 |
D. |
矩形 |
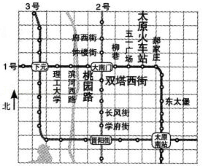
如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为,表示桃园路的点的坐标为,则表示太原火车站的点(正好在网格点上)的坐标是 .
如图是一组有规律的图案,它们是由边长相同的小正方形组成,其中部分小正方形涂有阴影,依此规律,第个图案中有 个涂有阴影的小正方形(用含有的代数式表示).

如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为 .

每年5月的第二周为"职业教育活动周",今年我省开展了以"弘扬工匠精神,打造技能强国"为主题的系列活动.活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加"职教体验观摩"活动,相关职业技术人员进行了现场演示,活动后该校教务处随机抽取了部分学生进行调查:"你最感兴趣的一种职业技能是什么?"并对此进行了统计,绘制了统计图(均不完整).请解答以下问题:
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对"工业设计"最感兴趣的学生有多少人?
(3)要从这些被调查的学生中,随机抽取一人进行访谈,那么正好抽到对"机电维修"最感兴趣的学生的概率是 .

请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .
我省某苹果基地销售优质苹果,该基地对需要送货且购买量在 (含 和 的客户有两种销售方案(客户只能选择其中一种方案)
方案 :每千克5.8元,由基地免费送货.
方案 :每千克5元,客户需支付运费2000元.
(1)请分别写出按方案 ,方案 购买这种苹果的应付款 (元 与购买量 之间的函数表达式;
(2)求购买量 在什么范围时,选用方案 比方案 付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢 的长度相同,均为 , 的倾斜角为 , ,支撑角钢 , 与底座地基台面接触点分别为 、 , 垂直于地面, 于点 .两个底座地基高度相同(即点 , 到地面的垂直距离相同),均为 ,点 到地面的垂直距离为 ,求支撑角钢 和 的长度各是多少 (结果保留根号).

综合与实践
问题情境
在综合与实践课上,老师让同学们以"菱形纸片的剪拼"为主题开展数学活动,如图1,将一张菱形纸片 沿对角线 剪开,得到 和 .
操作发现
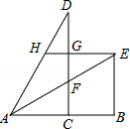
(1)将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图2所示的△ ,分别延长 和 交于点 ,则四边形 的形状是 ;
(2)创新小组将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图3所示的△ ,连接 , ,得到四边形 ,发现它是矩形,请你证明这个结论;
实践探究
(3)缜密小组在创新小组发现结论的基础上,量得图3中 , ,然后提出一个问题:将△ 沿着射线 方向平移 ,得到△ ,连接 , ,使四边形 恰好为正方形,求 的值,请你解答此问题;
(4)请你参照以上操作,将图1中的 在同一平面内进行一次平移,得到△ ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.





 粤公网安备 44130202000953号
粤公网安备 44130202000953号