吉林省吉林市高三第三次模拟考试理科数学试卷
已知随机变量ξ服从正态分布N(1,σ2),若P(ξ>3)=0.023,则P(-1≤ξ≤3)等于( )
| A.0.977 | B.0.954 | C.0.628 | D.0.477 |
现有三个函数:① ,②
,② ,③
,③ 的图象(部分)如下:
的图象(部分)如下:


则按照从左到右图象对应的函数序号安排正确的一组是( )
| A.①②③ | B.③①② | C.②①③ | D.③②① |
边长为4的正方形ABCD的中心为O,以O为圆心,1为半径作圆,点M是圆O上的任意一点,
点N是边AB、BC、CD上的任意一点(含端点),则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
已知边长为1的等边三角形 与正方形
与正方形 有一公共边
有一公共边 ,二面角
,二面角 的余弦
的余弦
值为 ,若A、B、C、D、E在同一球面上,则此球的体积为( )
,若A、B、C、D、E在同一球面上,则此球的体积为( )
A. B.
B. C.
C. D.
D.
若存在直线l与曲线 和曲线
和曲线 都相切,则称曲线
都相切,则称曲线 和曲线
和曲线 为“相关曲线”,有下列四个命
为“相关曲线”,有下列四个命
题:
①有且只有两条直线l使得曲线 和曲线
和曲线 为“相关曲线”;
为“相关曲线”;
②曲线 和曲线
和曲线 是“相关曲线”;
是“相关曲线”;
③当 时,曲线
时,曲线 和曲线
和曲线 一定不是“相关曲线”;
一定不是“相关曲线”;
④必存在正数 使得曲线
使得曲线
 和曲线
和曲线
 为“相关曲线”.
为“相关曲线”.
其中正确命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
从5名志愿者中选出4人,分别参加两项公益活动,每项活动2人,则不同安排方案的种数
为 .(用数字作答)
已知直线 与抛物线
与抛物线 交于A,B两点,点P为直线l上一动点,M,N是抛物线C上两个动点,若
交于A,B两点,点P为直线l上一动点,M,N是抛物线C上两个动点,若 ,
, , 则△PMN的面积的最大值为 .
, 则△PMN的面积的最大值为 .
(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,设S为△ABC的面积,满足 .
.
(Ⅰ)求B;
(Ⅱ)若 ,设
,设 ,
, ,求函数
,求函数 的解析式和最大值.
的解析式和最大值.
(本小题满分12分)某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体
1000名学生中随机抽取了若干名学生的体检表,并得到如下直方图:
(Ⅰ)若直方图中前三组的频率成等比数列,后四组的频率成等差数列,试估计全年级视力在5.0以下的
人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有
关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
| 年级名次 是否近视 |
1~50 |
951~1000 |
| 近视 |
41 |
32 |
| 不近视 |
9 |
18 |
根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(Ⅲ)在(Ⅱ)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良
好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为 ,求
,求 的分布列和数学期
的分布列和数学期
望.
附:
| P(K2≥k) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |

(本小题满分12分)如图,在多面体ABCDEF中,正方形 与梯形
与梯形 所在平面互相
所在平面互相
垂直,已知 ,
, ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 的直线l与椭圆C相交于A,B两点,且△
的直线l与椭圆C相交于A,B两点,且△ 的周长为
的周长为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作与直线l平行的直线m,且直线m与抛物线
作与直线l平行的直线m,且直线m与抛物线 交于P、Q两点,若A、P在x轴
交于P、Q两点,若A、P在x轴
上方,直线PA与直线QB相交于x轴上一点M,求直线l的方程.
(本小题满分12分)设函数 .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)如果对所有的 ≥0,都有
≥0,都有 ≤
≤ ,求
,求 的最小值;
的最小值;
(Ⅲ)已知数列 中,
中, ,且
,且 ,若数列
,若数列 的前n项和为
的前n项和为 ,求证:
,求证: .
.
(本小题满分10分)选修4—1:几何证明选讲
如图,在△ABC中, ,以
,以 为直径的⊙O交
为直径的⊙O交 于
于 ,过点
,过点 作⊙O的切线交
作⊙O的切线交 于
于 ,
,
交⊙O于点 .
.
(Ⅰ)证明: 是
是 的中点;
的中点;
(Ⅱ)证明: .
.
(本小题满分10分)选修4—4:坐标系与参数方程
在极坐标系中曲线 的极坐标方程为
的极坐标方程为 ,点
,点 . 以极点O为原点,以极轴为x
. 以极点O为原点,以极轴为x
轴正半轴建立直角坐标系.斜率为 的直线l过点M,且与曲线C交于A,B两点.
的直线l过点M,且与曲线C交于A,B两点.
(Ⅰ)求出曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)求点M到A,B两点的距离之积.
 ,集合
,集合 ,集合
,集合 ,则图中阴影部分所表示的集合是( )
,则图中阴影部分所表示的集合是( )




 ( )
( )



 是第四象限角,且
是第四象限角,且 ,则
,则 ( )
( )

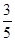
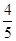
 满足
满足 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( ) 等于( )
等于( )



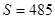 ,则判断框内的条件是( )
,则判断框内的条件是( )



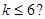





 是公比不为1的等比数列,其前n项和为
是公比不为1的等比数列,其前n项和为 ,若
,若 成等差数列,则
成等差数列,则 .
. 的图象上各点向右平移
的图象上各点向右平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则 的最小值为 .
的最小值为 . ,
, ,
, .
. 时,若
时,若 对任意
对任意 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围; 时,求函数
时,求函数 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号