北京市东城区高三5月综合练习二文科数学试卷
设点 ,则“
,则“ 且
且 ”是“点
”是“点 在直线
在直线 上”的( )
上”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
已知正方体 的棱长为
的棱长为 ,
, ,
, 分别是边
分别是边 ,
, 的中点,点
的中点,点 是
是 上的动点,过点
上的动点,过点 ,
, ,
, 的平面与棱
的平面与棱 交于点
交于点 ,设
,设 ,平行四边形
,平行四边形 的面积为
的面积为 ,设
,设 ,则
,则 关于
关于 的函数
的函数 的解析式为( )
的解析式为( )
A. , , |
B. |
C. |
D. , , |
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
设函数 ,
, 的两个的零点为
的两个的零点为 ,
, ,且方程
,且方程 有两个不同的实根
有两个不同的实根 ,
, .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数 .
.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
如图,△ 是边长为
是边长为 的正三角形,以
的正三角形,以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ;以
;以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ;以
;以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ,则
,则 .如此继续以
.如此继续以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ,
, ,当弧长
,当弧长 时,
时, .
.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为 ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有 个白球和
个白球和 个红球的盒子中一次性摸出
个红球的盒子中一次性摸出 球(这些球除颜色外
球(这些球除颜色外
完全相同),如果摸到的是 个红球,即为中奖.
个红球,即为中奖.
试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, 为
为 上一点,四边形
上一点,四边形 为矩形,
为矩形, ,
, ,
, .
.
(Ⅰ)若 ,且
,且 ∥平面
∥平面 ,求
,求 的值;
的值;
(Ⅱ)求证: 平面
平面 .
.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
已知等比数列 的前
的前 项和
项和 ,且
,且 成等差数列.
成等差数列.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 是首项为
是首项为 ,公差为
,公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 ,求满足
,求满足 的最大正整数
的最大正整数 .
.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
已知椭圆 上的左、右顶点分别为
上的左、右顶点分别为 ,
, ,
, 为左焦点,且
为左焦点,且 ,又椭圆
,又椭圆 过点
过点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)点 和
和 分别在椭圆
分别在椭圆 和圆
和圆 上(点
上(点 除外),设直线
除外),设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,若
,若 ,证明:
,证明: ,
, ,
, 三点共线.
三点共线.
来源:2015届北京市东城区高三5月综合练习二文科数学试卷
 ,集合
,集合 ,
, ,如图阴影部分所表示的集合为( )
,如图阴影部分所表示的集合为( )




 为纯虚数,则实数
为纯虚数,则实数 的值为( )
的值为( )



 ,那么圆心坐标为( )
,那么圆心坐标为( )



 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )








 ,
, 满足不等式组
满足不等式组 则
则 的最大值为( )
的最大值为( )



 上一点
上一点
 ,则
,则 ,点
,点 的距离为 .
的距离为 .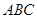 中,已知
中,已知 , 那么
, 那么 .
. 的最大值为 .
的最大值为 . ,
, 满足
满足

 ,则向量
,则向量 的夹角为 .
的夹角为 . ,
, .
. ,且
,且 ,求
,求 的值;
的值;
 ,求
,求 的最大值.
的最大值. ,
, ,(
,( ,
, 为常数).
为常数). 在
在 处的切线过点
处的切线过点 ,求
,求 的导函数为
的导函数为 ,若关于
,若关于 的方程
的方程 有唯一解,求实数
有唯一解,求实数 ,若函数
,若函数 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于 ,求实数
,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号