湖南省益阳市高三四月调研考试理科数学试卷
给出下列两个命题:命题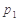 :
: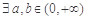 ,当
,当 时,
时,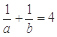 ;命题
;命题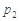 :函数
:函数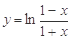 是偶函数.则下列命题是真命题的是
是偶函数.则下列命题是真命题的是
A.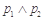 |
B.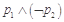 |
C.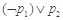 |
D.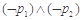 |
十字路口车流量被定义为单位时间内通过十字路口的车辆数,小张上班经过的某十字路口某时间段内车流量变化近似符合函数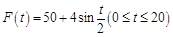 (
( 的单位是辆/分,
的单位是辆/分, 的单位是分),则下列时间段内车流量增加的是
的单位是分),则下列时间段内车流量增加的是
A.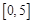 |
B.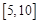 |
C.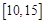 |
D.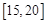 |
已知函数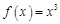 的图象为曲线
的图象为曲线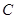 ,给出以下四个命题:
,给出以下四个命题:
①若点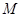 在曲线
在曲线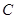 上,过点
上,过点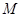 作曲线
作曲线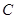 的切线可作一条且只能作一条;
的切线可作一条且只能作一条;
②对于曲线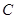 上任意一点
上任意一点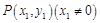 ,在曲线
,在曲线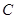 上总可以找到一点
上总可以找到一点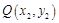 ,使
,使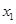 和
和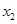 的等差中项是同一个常数;
的等差中项是同一个常数;
③设函数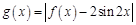 ,则
,则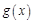 的最小值是0;
的最小值是0;
④若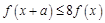 在区间
在区间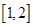 上恒成立,则a的最大值是1.其中真命题的个数是
上恒成立,则a的最大值是1.其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).在极坐标系 (与直角坐标系
为参数).在极坐标系 (与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的极坐标方程为
的极坐标方程为 ,若直线
,若直线 平分圆
平分圆 的周长,则
的周长,则 .
.
如图是某几何体的三视图,正视图和侧视图都是等腰直角三角形,俯视图是边长为3的正方形,则此几何体的体积等于 .
已知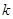 为合数,且
为合数,且 ,当
,当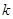 的各数位上的数字之和为质数时,称此质数为
的各数位上的数字之和为质数时,称此质数为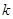 的“衍生质数”.
的“衍生质数”.
(1)若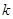 的“衍生质数”为2,则
的“衍生质数”为2,则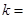 ;
;
(2)设集合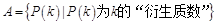 ,
,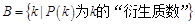 ,则集合
,则集合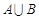 中元素的个数是 .
中元素的个数是 .
(本小题满分12分)在△ABC中,内角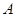 ,
,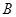 ,
,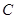 的对边长分别为a,b,c,且
的对边长分别为a,b,c,且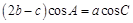 .
.
(Ⅰ)求角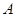 的大小;
的大小;
(Ⅱ)若a=3,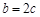 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分12分)某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为 ,且相互间没有影响.
,且相互间没有影响.
(Ⅰ)求选手甲进入复赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为,试求的分布列和数学期望.
(本小题满分12分)如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2AD=2,E为AB的中点,F为D1E上的一点,D1F=2FE.
(Ⅰ)证明:平面
 平面
平面 ;
;
(Ⅱ)求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分13分)已知数列 的首项
的首项 ,其前
,其前 和为
和为 ,且满足:
,且满足: (
( N*).
N*).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)对任意的 N*,
N*, ,求实数a的取值范围.
,求实数a的取值范围.
(本小题满分13分)已知M( ,0),N(2,0),曲线C上的任意一点P满足:
,0),N(2,0),曲线C上的任意一点P满足: .
.
(Ⅰ)求曲线C的方程;
(Ⅱ)设曲线C与x轴的交点分别为A、B,过N的任意直线(直线与x轴不重合)与曲线C交于R、Q两点,直线AR与BQ交于点S.问:点S是否在同一直线上?若是,请求出这条直线的方程;若不是,请说明理由.
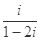 (
(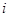 为虚数单位)在复平面内对应的点位于
为虚数单位)在复平面内对应的点位于  ,
, ,若
,若 ,则
,则 的值为
的值为



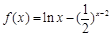 的零点为
的零点为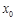 , 则
, 则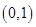
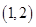
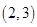
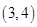
 ,则二项式
,则二项式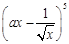 展开式中含
展开式中含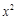 项的系数是
项的系数是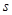 的值为70,则判断框内可填入的条件是
的值为70,则判断框内可填入的条件是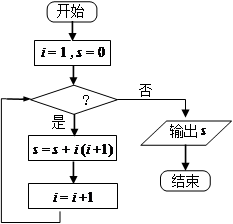
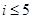
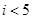
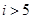
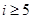
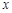 、
、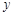 满足不等式组
满足不等式组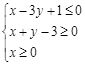 ,则
,则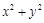 的最小值是
的最小值是
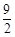
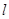 :
: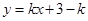 与双曲线:
与双曲线: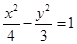 有交点,则实数
有交点,则实数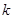 的取值范围是
的取值范围是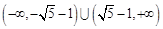
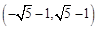

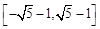
 R,
R, ,
, ,则M的最大值是 .
,则M的最大值是 . 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 交圆
交圆 于点
于点 ,圆
,圆 ,则
,则
 的导函数为
的导函数为 ,对任意
,对任意 ,不等式
,不等式 恒成立,则
恒成立,则 的最大值为 .
的最大值为 . (其中
(其中 为常数).
为常数). 时,求函数的单调区间;
时,求函数的单调区间; 时,对于任意大于1的实数
时,对于任意大于1的实数 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围;
的取值范围; 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且 .求证:
.求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号