广东省汕头市潮南区高三5月高考模拟理科数学试卷
通过随机询问110名大学生是否爱好某项运动,得到如下的列联表
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由上表算得 ,因此得到的正确结论是( )
,因此得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
“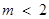 ”是“一元二次不等式
”是“一元二次不等式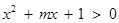 的解集为R”的( )
的解集为R”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设F是双曲线 的左焦点,A(1,4),P是双曲线右支上的动点,则|PF| +|PA|的最小值为( )
的左焦点,A(1,4),P是双曲线右支上的动点,则|PF| +|PA|的最小值为( )
| A.5 | B. |
C.7 | D.9 |
如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
| A.84 | B.72 | C.64 | D.56 |
已知f(x)=x2,g(x)=|x﹣1|,令f1(x)=g(f(x)),fn+1(x)=g(fn(x)),则方程f2015(x)=1解的个数为( )
| A.2014 | B.2015 | C.2016 | D.2017 |
等差数列{an}前n项和为Sn,公差d<0,若S20>0,S21<0,,当Sn取得最大值时,n的值为 .
给出下列六种图象变换方法:
①图象上所有点的横坐标缩短到原来的 ,纵坐标不变;
,纵坐标不变;
②图象上所有点的横坐标伸长到原来的2倍,纵坐标不变;
③图象向右平移 个单位;④图象向左平移
个单位;④图象向左平移 个单位;
个单位;
⑤图象向右平移 个单位;⑥图象向左平移
个单位;⑥图象向左平移 个单位.
个单位.
请用上述变换中的两种变换,将函数 的图象变换到函数
的图象变换到函数 的图象,那么这两种变换的序号依次是 (填上一种你认为正确的答案即可).
的图象,那么这两种变换的序号依次是 (填上一种你认为正确的答案即可).
(坐标系与参数方程选做题)已知直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,点
,点 是直线
是直线 上的一个动点,过点
上的一个动点,过点 作曲线
作曲线 的切线,切点为
的切线,切点为 ,则
,则 的最小值为 .
的最小值为 .
(平面几何选做题)已知 为半圆
为半圆 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 作半圆的切线
作半圆的切线 ,过点
,过点 作
作 于
于 ,交半圆
,交半圆 于点
于点 ,
, ,则
,则 的长为 .
的长为 .
在平面直角坐标系 中,以
中,以 轴为始边,锐角
轴为始边,锐角 的终边与单位圆在第一象限交于点A,且点A的纵坐标为
的终边与单位圆在第一象限交于点A,且点A的纵坐标为 ,锐角
,锐角 的终边与射线x-7y=0(
的终边与射线x-7y=0( )重合.
)重合.
(1)求 的值;
的值;
(2)求 的值.
的值.
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分14分)如图,直角梯形 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥ ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点 ,使
,使 // 平面
// 平面 ?若存在,求出
?若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题满分14分)在单调递增数列 中,
中, ,
, ,且
,且 成等差数列,
成等差数列, 成等比数列,
成等比数列, .
.
(1)分别计算 ,
, 和
和 ,
, 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将 用
用 表示);
表示);
(3)设数列 的前
的前 项和为
项和为 ,证明:
,证明: ,
,
(本小题满分14分)如图,椭圆
 过点
过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,离心率
,离心率 ,
, 是直x=上的两个动点,且
是直x=上的两个动点,且 .
.
(1)求椭圆的方程;
(2)求 的最小值;
的最小值;
(3)以 为直径的圆
为直径的圆 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
 ,则
,则 在复平面上对应的点在( )
在复平面上对应的点在( ) ,
, ,且
,且 ,则
,则 ( )
( )




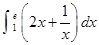 ]
] 的展开式中所有二项式系数之和为64,则展开式的常数项为 .
的展开式中所有二项式系数之和为64,则展开式的常数项为 . 的点共有 个.
的点共有 个.
 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由; ,试判断函数
,试判断函数 在
在 上的符号,并证明:
上的符号,并证明:
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号