（本小题满分14分）如图，直角梯形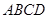
与等腰直角三角形
所在的平面互相垂直．
∥
，
，
，
．
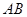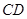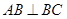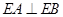（1）求证：
；
（2）求直线
与平面
所成角的正弦值；
（3）线段
上是否存在点
，使// 平面
？若存在，求出
；若不存在，说明理由．
．对任意
，
恒成立，若
，求
的范围．
的最小正周期；
为第三象限角，问是否存在这样的实数m，使得
、
是关于
的方程
的两个根，若存在，求出实数m，若不存在，请说明理由.
的定义域与值域相关知识点
推荐套卷
（本小题满分14分）如图，直角梯形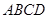与等腰直角三角形所在的平面互相垂直．∥，，，．
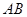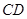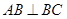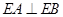（1）求证：；
（2）求直线与平面所成角的正弦值；
（3）线段上是否存在点，使// 平面？若存在，求出；若不存在，说明理由．
粤公网安备 44130202000953号