江苏省无锡市锡山区九年级上学期期末考试数学试卷
已知一组数据:15,13,15,16,17,16,14,15,则极差与众数分别是 ( )
| A.4,15 | B.3,15 | C.4,16 | D.3,16 |
下列一元二次方程中,两实根之和为1的是 ( )
| A.x2—x+1=0 | B.x2+x—3=0 |
| C.2 x2-x-1=0 | D.x2-x-5=0 |
若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD一定是( )
| A.矩形 | B.菱形 |
| C.对角线互相垂直的四边形 | D.对角线相等的四边形 |
已知圆柱的底面半径为3cm,母线长为6cm,则圆柱的侧面积是( )
| A.36cm2 | B.36πcm2 | C.18cm2 | D.18πcm2 |
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面3个结论:①AD=CD;②BD=BC;③AB=2BC,其中正确结论的个数是( )
| A.3 | B.2 | C.1 | D.0 |
二次函数y=ax2+bx+c的图像如图所示,当函数值y<0时,x的取值范围为 ( )
| A.x<—1或x>3 | B.—1<x<3 | C.x≤—1或x≥3 | D.—1≤x≤3 |
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
A. r2 r2 |
B. |
C. r2 r2 |
D. r2 r2 |
如图,在3×3的网格图中,在不添加其他线的情况下,不是正方形的矩形个数为( )
| A.14个 | B.22个 |
| C.36个 | D.以上都不正确 |
将 y=x2-2x+3 化成 y=a(x-h)2+k 的形式,则 y=_____________.
如果关于x的一元二次方程x2-2x+m-1=0的一根为3,则另一根为_____________.
某工厂今年3月份的产值为50万元,4月份和5月份的总产值为132万元.若设平均每月增长的百分率为x,则列出的方程为:__________________________.
如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6cm,DE=5cm,则CD的长为___________cm.
如图,□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于_________.
如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_________________cm.
在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,则∠BDC的度数为___________________.
(本题共有2小题,每小题4分,共8分)
(1)计算:( )-1-(2015-
)-1-(2015- )0―|-2|; (2)化简:
)0―|-2|; (2)化简: -(a-2).
-(a-2).
解方程或不等式组(本题共有2小题,每小题4分,共8分)
(1)解方程:x2-5x-4=0;
(2)解不等式组: .
.
已知:如图,菱形ABCD中,∠A=60°,F是CD的中点,过C作CE∥BD,且DE⊥CE.求证:BF =DE.
在1、2、3、4、5这五个数中,先任意取一个数a,然后在余下的数中任意取出一个数b,组成一个点(a,b).求组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率.(请用“画树状图”或“列表”等方法写出分析过程)
如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)
(1)图中AC边上的高为_________个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:
①以点C为位似中心,作△DEC∽△ABC,且相似比为1∶2;
②以AB为一边,作矩形ABMN,使得它的面积恰好为△ABC的面积的2倍.
如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米,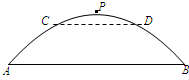
(1)建立恰当的坐标系,求出抛物线的解析式;
(2)当洪水泛滥,水面上升,若拱桥的水面跨度只有30米时,则必须马上采取紧急措施.现已知拱顶P离水面CD的距离只有4米,问:是否要采取紧急措施?并说明理由.
某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
| 销售单价x(元) |
50 |
60 |
70 |
80 |
| 销售数量y(万件) |
5.5 |
5 |
4.5 |
4 |
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额-总进货价-其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.
(1)求∠DMP的度数;
(2)求△BPE的面积.
如图,边长为15cm的等边△ABC的顶点B、C都在直线l上,现将一块直角三角尺DEF按如图位置摆放,其中DE=EF=12cm,∠DEF=90°,E、F在直线l上,且F与B重合.若将三角尺DEF沿直线l以3cm/s的速度向右移动,设运动时间为t(s).
(1)请直接写出三角尺DEF的顶点D落在△ABC内部(不含边上)时,时间t的取值范围:______________;
(2)在运动过程中,设△DEF与△ABC的重叠部分面积为S(cm2),试求在点F到达点C之前,S与t的函数关系式,并写出自变量t的取值范围.

 中自变量x的取值范围是( )
中自变量x的取值范围是( )


 ,
, ,π,0.10110中任取一个数,取到无理数的概率是__________.
,π,0.10110中任取一个数,取到无理数的概率是__________. ,AB=AC,AH⊥BC于H,D为AC的中点,BD交AH于点M.
,AB=AC,AH⊥BC于H,D为AC的中点,BD交AH于点M.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号