如图，在平面直角坐标系中，点A的坐标为（12，−8），点B、C在x轴上，tan∠ABC＝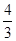
，AB＝AC，AH⊥BC于H，D为AC的中点，BD交AH于点M．
（1）求过B、C、D三点的抛物线的解析式，并求出抛物线顶点E的坐标；
（2）过点E且平行于AB的直线l交y轴于点G，若将（2）中的抛物线沿直线l平移，平移后的抛物线交y轴于点F，顶点为E′（点E′在y轴右侧）．是否存在这样的抛物线，使△E′FG为等腰三角形？若存在，请求出此时顶点E’的坐标；若不存在，请说明理由．
相关试题
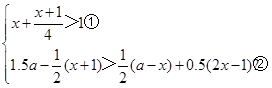只有一个整数解。
的方程
的解，求实数
的取值范围．如图，一次函数的图象与反比例函数y1＝－
(x<0)的图象相交于正A点，与y轴、x轴分别相交于B、C两点，且C(2，0)．当x<－1时，一次函数值大于反比例函数值；当x>－1时，一次函数值小于反比例函数值
（1）求一次函数的解析式
（2）设函数y2＝
(x>0)的图象与y1＝－(x<0)的图象关于y轴对称，在y2＝(x>0)的图象上取一点P(P点的横坐标大于2)，过P作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标
为调动销售人员的积极性，A、B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1～6月份的销售额如下表：
| 月份 销售额: |
销售额（单位：元） |
|||||
| 1月 |
2月 |
3月 |
4月 |
5月 |
6月 |
|
| 小李（A公司） |
11600 |
12800 |
14000 |
15200 |
16400 |
17600 |
| 小张（B公司 |
7400 |
9200 |
11000 |
12800 |
14600 |
16400 |
（1）请问小李与小张3月份的工资各是多少
（2）小李1～6月份的销售额
与月份
的函数关系式是
小张1～6月份的销售额
也是月份的一次函数，请求出与的函数关系式
（3）如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资
并把解集在数轴上表示出来相关知识点
推荐套卷
粤公网安备 44130202000953号