甘肃省河西三校普通高中高三上学期第一次联考理科数学试卷
“ ”是“
”是“ ”的( )条件
”的( )条件
| A.充分不必要 | B.必要不充分 | C.充分必要 | D.既不充分也不必要 |
设 与
与 是定义在同一区间[a,b]上的两个函数,若函数
是定义在同一区间[a,b]上的两个函数,若函数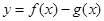 在
在 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”.若
称为“关联区间”.若 与
与 在[0,3]上是“关联函数”,则m的取值范围是( )
在[0,3]上是“关联函数”,则m的取值范围是( )
A. |
B.[-1,0] | C.(-∞,-2] | D. |
设函数 在R上可导,其导函数为
在R上可导,其导函数为 ,且函数
,且函数 的图象如图所示,则下列结论中一定成立的是( )
的图象如图所示,则下列结论中一定成立的是( )
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
已知函数 ,
, ,若至少存在一个
,若至少存在一个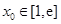 ,使
,使 成立,则实数a的范围为( )
成立,则实数a的范围为( )
A.[ ,+∞) ,+∞) |
B.(0,+∞) | C.[0,+∞) | D.( ,+∞) ,+∞) |
将5位志愿者分成3组,其中两组各2人,另一组1人,分赴青奥会的三个不同场馆服务,不同的分配方案有 种(用数字作答).
设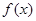 是定义在R上的偶函数,且对于
是定义在R上的偶函数,且对于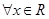 恒有
恒有 ,已知当
,已知当 时,
时, 则
则
(1)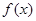 的周期是2;
的周期是2;
(2)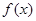 在(1,2)上递减,在(2,3)上递增;
在(1,2)上递减,在(2,3)上递增;
(3)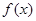 的最大值是1,最小值是0;
的最大值是1,最小值是0;
(4)当 时,
时,
其中正确的命题的序号是 .
(本小题满分12分)设命题p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 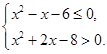 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若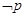 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
(本小题满分12分)某市公租房的房源位于 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
(1)恰有2人申请 片区房源的概率;
片区房源的概率;
(2)申请的房源所在片区的个数 的分布列和期望.
的分布列和期望.
(本小题满分12分)设函数 ,曲线
,曲线 在点P(1,0)处的切线斜率为2.
在点P(1,0)处的切线斜率为2.
(1)求a,b的值;
(2)证明: .
.
(本小题满分12分)为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
| 新能源汽车补贴标准 |
|||
| 车辆类型 |
续驶里程 (公里) (公里) |
||
 |
 |
 |
|
| 纯电动乘用车 |
 万元/辆 万元/辆 |
 万元/辆 万元/辆 |
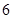 万元/辆 万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了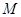 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 合计 |
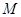 |
 |
(1)求 ,
, ,
, ,
,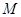 的值;
的值;
(2)若从这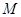 辆纯电动乘用车中任选
辆纯电动乘用车中任选 辆,求选到的
辆,求选到的 辆车续驶里程都不低于
辆车续驶里程都不低于 公里的概率;
公里的概率;
(3)若以频率作为概率,设 为购买一辆纯电动乘用车获得的补贴,求
为购买一辆纯电动乘用车获得的补贴,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)已知函数 ,其中a,b∈R,e=2.718 28 为自然对数的底数.
,其中a,b∈R,e=2.718 28 为自然对数的底数.
(1)设 是函数
是函数 的导函数,求函数g(x)在区间[0,1]上的最小值;
的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数 在区间(0,1)内有零点,求a的取值范围.
在区间(0,1)内有零点,求a的取值范围.
(本小题满分10分)选修4-1:几何证明选讲
如图, 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点

(Ⅰ)证明: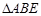 ∽△
∽△ ;
;
(Ⅱ)若 的面积
的面积 ,求
,求 的大小.
的大小.
(本小题满分10分)选修4—4:坐标系与参数方程
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4, ),若直线
),若直线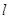 过点P,且倾斜角为
过点P,且倾斜角为 ,圆C以M为圆心,4为半径。
,圆C以M为圆心,4为半径。
(1)求直线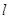 的参数方程和圆C的极坐标方程。
的参数方程和圆C的极坐标方程。
(2)试判定直线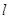 与圆C的位置关系。
与圆C的位置关系。
 则
则 ( )
( )



 命题
命题 ,则下列命题中为真命题的是:( )
,则下列命题中为真命题的是:( )

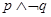

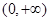 为增函数的是( )
为增函数的是( )



 的零点个数为( )
的零点个数为( )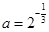 ,
, ,则( )
,则( )
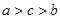


 在R上为减函数,则( )
在R上为减函数,则( )



 的图象大致为( )
的图象大致为( )
 与曲线
与曲线 相切,则b的值为( )
相切,则b的值为( )
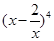 的展开式中的常数项为______________(用数字作答)
的展开式中的常数项为______________(用数字作答) ,且P
,且P ,P
,P ,则P(
,则P( )= .
)= .

 的不等式
的不等式 
 的图象恒在函数
的图象恒在函数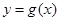 的上方,求实数
的上方,求实数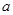 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号