暖春三月,贴心开学测 初三数学第五套
常见的五角星绕中心旋转一个最小的角度α后,即可与自身重合,则α等于( )
| A.90° | B.180° | C.60° | D.72° |
下列实验中,概率最大的是( )
| A.抛掷一枚质地均匀的硬币,出现正面的概率 |
| B.抛掷一枚质地均匀的正方体骰子(六个面分别刻有数字1到6),掷出的点数为奇数的概率 |
| C.在一副洗匀的扑克(背面朝上)中任取一张,恰好为方块的概率 |
| D.三张同样的纸片,分别写有数字2、3、4,和匀后背面向上,任取一张恰好为偶数的概率 |
手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不一定相似的是( )
A. |
B. |
C. |
D. |
若c(c≠0)为关于x的一元二次方程x2+bx+c=0的根,则c+b的值为( )
| A.1 | B.﹣1 | C.2 | D.﹣2 |
从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2,则原来正方形的面积为( )
| A.100cm2 | B.121cm2 | C.144cm2 | D.169cm2 |
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ﹣ ﹣ |
B. ﹣ ﹣ |
C.π﹣ |
D.π﹣ |
如图,Rt△BAO的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△BAO绕原点O按顺时针方向旋转90°后得到△B′A′O,则点B的对应点B′的坐标是( )

| A.(1,﹣2) | B.(2,﹣ ) ) |
C.(﹣2,1) | D.(2,﹣1) |
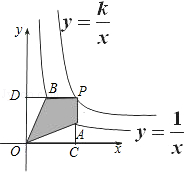
两个反比例函数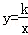 和
和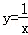 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在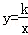 的图象上,PC⊥x轴于点C,交
的图象上,PC⊥x轴于点C,交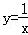 的图象于点A,PD⊥y轴于点D,交
的图象于点A,PD⊥y轴于点D,交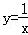 的图象于点B,当点P在
的图象于点B,当点P在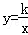 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.
其中一定正确的是 (把你认为正确结论的序号都填上).
已知抛物线y1=a(x﹣1)2+4与直线y2=x+1的一个交点的横坐标是2.
(1)求a的值;
(2)请在所给的坐标系中,画出函数y1=a(x﹣1)2+4与y2=x+1的图象,并根据图象,直接写出y1≥y2时x的取值范围.
已知二次函数y=a(x﹣2)2﹣a(x﹣2)(a为常数,且a≠0.)
(1)求证:不论a为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC的面积等于2时,求a的值.
某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
今年入秋以来,我国越来越多的城市出现雾霾天气,由于雾霾天气空中浮游大量粉尘和烟粒等有害物质,能对人体的呼吸道造成伤害,为了预防疾病,在雾霾天气人们出行大多选择戴口罩出行,导致甲型和乙型口罩的销售量急速增加.某药店这两种口罩的月销售从九月份的2000个增加到11月份的3380个.
(1)求该药店9月份到11月份的月销售量的平均增长率;
(2)生产商看到口罩的销售情况决定再招30名工人扩大生产.已知一名工人每天能生产100个甲型口罩或60个乙型口罩.若要求这30名工人每天生产的口罩数量不低于2500个,并且生产乙型口罩的人数不低于生产甲型口罩人数的一半,该生产商应该如何安排这30名工人进行生产?
实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).

(1)作∠BCA的平分线,交AB于点O;
(2)以O为圆心,OB为半径作圆.
综合运用:在你所作的图中,
(1)AC与⊙O的位置关系是 (直接写出答案)
(2)若BC=6,AB=8,求⊙O的半径.
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.

(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 ;
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 ;
(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
已知二次函数y=﹣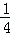 x2+
x2+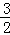 x的图象如图.
x的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式.




 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( ) 化成y=a(x+m)2+n的形式是( )
化成y=a(x+m)2+n的形式是( )



 ﹣2)0+|2﹣
﹣2)0+|2﹣ ×
× = .
= . 的长是 .
的长是 .
 ﹣1的图象如图,则关于x的分式方程
﹣1的图象如图,则关于x的分式方程
 )﹣1+20140﹣|
)﹣1+20140﹣| ﹣1|
﹣1| )2013(2+
)2013(2+ )2014+2×
)2014+2× +(﹣
+(﹣ ,求BC的长和∠B的正切值.
,求BC的长和∠B的正切值.

 的图象与一次函数y=x+2的图象交于点A(1,m),求反比例函数
的图象与一次函数y=x+2的图象交于点A(1,m),求反比例函数

 粤公网安备 44130202000953号
粤公网安备 44130202000953号