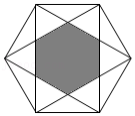
连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为
| A. |
|
B. |
|
C. |
|
D. |
|
一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .

以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,从一个大正方形中截去面积为 和 的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为

| A. |
|
B. |
|
C. |
|
D. |
|
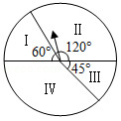
如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是
A. B. C. D.
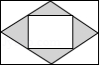
如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是
A. B. C. D.
小明将如图所示的转盘分成 是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连续偶数数字2,4,6, , (每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是 ,则 的取值为

A.36B.30C.24D.18
一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 .

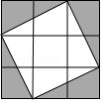
如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是
A. B. C. D.
中华文化源远流长, 如图是中国古代文化符号的太极图, 圆中的黑色部分和白色部分关于圆心中心对称 . 在圆内随机取一点, 则此点取黑色部分的概率是 .

如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,指针停止后落在黄色区域的概率是
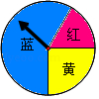
A. B. C. D.
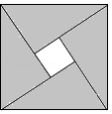
汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为 .现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为 .
正方形 的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形 内投一粒米,则米粒落在阴影部分的概率为
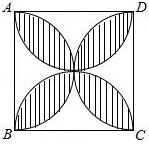
A. B. C. D.
如图,将一块菱形 硬纸片固定后进行投针训练.已知纸片上 于 , 于 , .若随意投出一针命中了菱形纸片,则命中矩形区域的概率是

A. B. C. D.