初中物理液体的压强的计算综合题

如图1所示，某打捞船打捞水中重物， $A$ 是重为 $600N$ 的动滑轮， $B$ 是定滑轮， $C$ 是卷扬机，卷杨机拉动钢丝绳通过滑轮组 $\mathit{AB}$ 竖直提升水中的重物，如图2所示，体积为 $0.3m^3$ 的重物浸没在水中，此时钢丝绳的拉力 $F$ 的大小为 $1.0\times {10}^{3}N$ ，摩擦、钢丝绳重、重物表面沾水的质量及水对重物的阻力均忽略不计， ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$ ， $g=10N/\mathit{kg}$ 。问：

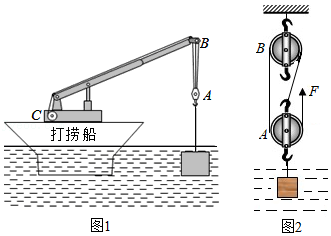
（1）当重物底部位于水面下 $5m$ 深处时，水对重物底部的压强是 　　 $\mathit{Pa}$ ；

（2）重物浸没在水中时受到三个力，其中浮力大小为 　　 $N$ ，重力大小为 　　 $N$ ；

（3）当重物逐渐露出水面的过程中，重物浸入水中的体积不断减小，打捞船浸入水中的体积不断变 　　；重物全部露出水面和浸没时相比，打捞船浸入水中的体积变化了 　　 $m^3$ ；

（4）重物全部露出水面后匀速上升了 $1m$ ，钢丝绳末端移动了 　　 $m$ 。此过程中滑轮组的机械效率是多少？

如图甲所示，薄壁圆柱形容器放在水平台上，容器的底面积 $S_{容}=100c{m}^2$ ，质量均匀的圆柱体物块上表面中央用足够长的细绳系住，悬挂于容器中。以恒定速度向容器中缓慢注水（每分钟注入 $100g)$ ，直至注满容器为止，细绳的拉力大小与注水时间的关系图像如图乙所示。 ${\rho }_{水}=1g/c{m}^3$ ，常数 $g=10N/\mathit{kg}$ ，物块不吸水，忽略细绳体积、液体扰动等其它次要因素。

（1）求注水前圆柱体物块的下表面到容器底部的距离 $L_1$ ；

（2）当细绳的拉力为 $0.9N$ 时，求水对物块下表面的压强；

（3）若改为以恒定速度向容器中缓慢注入另一种液体（每分钟注入 $100c{m}^3$ ， ${\rho }_{液}=1.5g/c{m}^3)$ ，直至 $9.4\mathit{min}$ 时停止。求容器底部所受液体压强 $p$ 与注液时间 $t_x$ 分钟 $(0⩽t_x⩽9.4)$ 的函数关系式。

解放前，我国经济很落后，一些地区过着极其原始的生活。如图所示，就是为了解决饮水问题，需要到很远地方挑水的示意图。为了防止道路不好水溅出桶外，在水面上覆盖木板（如图），若一个木板质量为 $500g$，密度为 $0.8\times {10}^3\mathit{kg}/m^3$，每个桶内水深 $30\mathit{cm}\left({\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3\right)$，求：

（1）桶底受到的水产生的压强；

（2）一个木板受到的浮力及静止时露出水面的体积；

（3）扁担与绳质量忽略不计，扁担长度 $1.5m$，每桶水总重 $180N$，扁担与肩膀接触点距离扁担右端 $55\mathit{cm}$，支撑手距离扁担左端也是 $55\mathit{cm}$，则支撑手受到的扁担产生的压力。

取一根内部横截面积为1平方厘米的直筒形塑料管，在底部扎上橡皮膜后，称得质量为2克。向管内倒入10克液体，再将它放入水中。放手后，观察到橡皮膜恰好变平，如图所示（管壁厚可以忽略）。

请回答：

（1）气管内液体的密度　 　（选填”大于“”等于“或”小于“ $)$水的密度。

（2）水对塑料管底部橡皮膜产生的压强大小。

（3）装有液体的塑料管受到的浮力大小。

如图甲所示，水平桌面上有个质量为 $2.5\mathit{kg}$，底面边长为 $0.5m$的正方体水槽，水槽内有一实心球。逐渐往水槽内加水，球受到的浮力 $F$与水深 $h$的关系如图乙所示，水深 $h=7\mathit{cm}$时，球刚好有一半体积浸入水中。不考虑水槽厚度，水的密度为 $1.0\times {10}^3\mathit{kg}/m^3$，求：

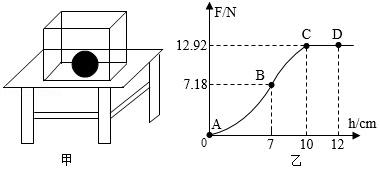
（1）实心球的体积和水深 $7\mathit{cm}$时水槽底部受到的水的压强；

（2）实心球的密度；

（3）实心球刚好离开水槽底部时水槽对水平桌面的压强。

雾炮车（又称多功能抑尘车）是利用高压原理向空气中喷洒颗粒格外细小的水雾，除去空气中过多的尘埃。某型号雾炮车的质量为 $10t$，它配备了一个体积为 $10m^3$的水箱。为了方便清洗，水箱底部有一个排水孔，排水孔盖子面积约为 $100c{m}^2$．

（1）空载时，若雾炮车轮与地面的总接触面积为 $0.8m^2$，则静止时车对水平地面的压强为多大？

（2）当水箱中水的深度为 $1m$时，排水孔盖子受到水的压力约为多大？

（3）如图所示，当雾炮车在水平路面上匀速行驶并不断向外喷水时，雾炮车发动机的输出功率如何变化？为什么？

质量为 $180\mathit{Kg}$的科考潜水器，在水下匀速下潜或加速下潜时受到水的阻力各不相同。若潜水器下潜时所受阻力与速度的关系如下表：

速度 $v/(m/s)$	1.2	1.2	1.2	1.3	1.4	1.5	1.6	1.7
阻力 $f\left(N\right)$	300	300	300	320	340	360	380	400

求：（1）潜水器在水面下 $30m$处，受到水的压强为多少？（水的密度为 $1.0\times {10}^3\mathit{Kg}/m^3)$

（2）向潜水器水仓中注入 $50\mathit{Kg}$水后，潜水器刚好以 $1.2m/s$的速度匀速下潜，求注水后潜水器的平均密度。

（3）写出潜水器加速下潜时，所受阻力 $f$与速度 $v$的关系式： $f=$　　。

如图所示，足够高的薄壁圆柱形容器放在水平桌面上，容器内水的质量为 $1\mathit{kg}$，水的深度为 $10\mathit{cm}$。实心圆柱体 $A$质量为 $400g$，底面积为 $20c{m}^2$，高度为 $16\mathit{cm}$。实心圆柱体 $B$质量为 $m_0$克 $(m_0$取值不确定），底面积为 $50c{m}^2$，高度为 $12\mathit{cm}$。实心圆柱体 $A$和 $B$均不吸水，已知 ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$，常数 $g$取 $10N/\mathit{kg}$。

（1）求容器的底面积。

（2）若将圆柱体 $A$竖直放入容器内，求静止时水对容器底部的压强 $p_1$。

（3）若将圆柱体 $B$竖直放入容器内，求静止时水对容器底部的压强 $p_2$与 $m_0$的函数关系式。

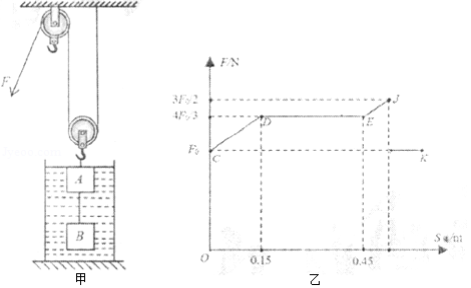
如图甲所示， $A$、 $B$为不同材料制成的体积相同的实心正方体，浸没在圆柱形容器的水中，容器内部底面积是正方体下表面积的4倍。沿固定方向缓慢匀速拉动绳子，开始时刻， $A$的上表面刚好与水面相平，滑轮组绳子自由端的拉力 $F$大小为 $F_0$， $F$随绳端移动距离 $s_{绳}$变化的图象如图乙所示。已知动滑轮的重力 $G_{动}=5N$， $g$取 $10N/\mathit{kg}$。除了连接 $A$、 $B$间的绳子承受拉力有一定限度外，其它绳子都不会被拉断。滑轮与轴的摩擦、绳的质量等次要因素都忽略不计。

（1）正方体 $A$、 $B$之间的绳子长度 $L_{绳}$是多少？

（2）正方体 $A$和 $B$的密度 ${\rho }_A$、 ${\rho }_B$分别是多少？

（3）整个过程中，水对容器底部压强的最大变化量△ $p$是多少？

如图1所示，置于水平地面的薄壁容器上面部分为正方体形状，边长 $l_1=4\mathit{cm}$，下面部分也为正方体形状，边长 $l_2=6\mathit{cm}$，容器总质量 $m_1=50g$，容器内用细线悬挂的物体为不吸水的实心长方体，底面积 $S_{物}=9c{m}^2$，下表面与容器底面距离 $l_3=2\mathit{cm}$，上表面与容器口距离 $l_4=1\mathit{cm}$，物体质量 $m_2=56.7g$。现往容器内加水，设水的质量为 $M$，已知 ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$， $g=10N/\mathit{kg}$。

（1）当 $M=58g$时，水面还没有到达物体的下表面，求此时容器对水平地面的压强；

（2）当 $M=194g$时，求水对容器底部的压力；

（3）当 $0⩽M⩽180g$时，求出水对容器底部的压力 $F$随 $M$变化的关系式，并在图2中作出 $F-M$图像。

如图甲所示，一个底面积为 $4\times {10}^{-2}{m}^2$的薄壁圆柱形容器置于水平地面上，装有 $0.3m$深的水。现将物体 $A$放人其中，物体 $A$漂浮于水面上，如图乙所示，此时容器底部受到水的压强比图甲增大了 $400\mathit{Pa}$．当再给物体 $A$施加一个竖直向下大小为 $4N$的力 $F$以后，物体 $A$恰好浸没水中静止（水未溢出），如图丙所示。 $({\rho }_{水}=1\times {10}^3\mathit{kg}/m^3$， $g$取 $10N/\mathit{kg})$求：

（1）容器中水的质量；

（2）物体 $A$放入前，容器底部受到水的压强；

（3）物体 $A$的密度。

我国正在研制的新一代“蛟龙号”深海探测器，目标探测深度 $11000m$，该深海探测器的全重为 $28t$。

（1）如果该深海探测器在未来的某一天来到大洋最深处马里亚纳海沟探测，下潜至某一深度处时，处于正上方海面处的科考船用声呐装置向“蛟龙号”发射声波，若从发出至接收到所用时间为 $12s$，则“蛟龙号”的实际下潜深度为多少米（已知声音在海水中的传播速度为 $1500m/s)$；

（2）若海面处的大气压为 $1.0\times {10}^5\mathit{Pa}$，海水密度为 $1.03\times {10}^3\mathit{kg}/m^3$，则“蛟龙号”下潜至 $11000m$时，所在位置处的压强为多少；

（3）若（1）问中“蛟龙号”处于悬浮状态，“蛟龙号”除空气仓部分的平均密度为 $7.0\times {10}^3\mathit{kg}/m^3$，试计算“蛟龙号”空气仓的体积（空气仓中的空气质量不计）。

2017年5月30日，“蛟龙号”载人潜水器在世界最深的马里亚纳海沟进行了本年度的第4潜，当地时间7时03分开始下潜，10时21分抵达预定 $6700m$深处，近距离在该深度处拍摄到了狮子鱼游弋的影像，获取到了基岩蚀变岩石、沉积物、生物和近底海水样品，已知“蛟龙号”的总体积为 $84m^3$． $({\rho }_{\mathit{海水}}=1.0\times {10}^3\mathit{kg}/m^3$， $g=10N/\mathit{kg})$

据此计算：

（1）“蛟龙号”潜水器下潜的速度为多大？（结果保留两位小数）

（2）“蛟龙号”潜水器未向水舱充水时的总质量为 $22t$，并且漂浮于海面上，求此时它排开海水的体积是多少？欲使“蛟龙号”完全浸没，至少应向水舱中充多少吨海水？

（3）狮子鱼头部上表面 $1\times {10}^{-4}{m}^2$的面积上受到的海水压力是多大？

（4）若将获取到的岩石样品取一小块，用天平和量筒测出它的质量和体积如图所示，则该岩石的密度为多少千克每立方米？

如图甲所示，一弹簧测力计下挂一圆柱体，将圆柱体从水面上方某一高度处匀速下降，然后将圆柱体逐渐浸入水中。整个过程中弹簧测力计的示数 $F$与圆柱体下降高度 $h$关系如图乙所示。 $(g=10N/\mathit{kg}$；水的密度约为 $1.0\times {10}^3\mathit{kg}/m^3)$

求：

（1）圆柱体的重力；

（2）当圆柱体刚好全部浸没时，下表面受到的水的压强；

（3）圆柱体的密度。

某实验小组在研究某种物质的属性时，日常需将物体浸没在煤油中保存，将体积为 $1\times {10}^{-3}{m}^3$、重 $6N$的该物体用细线系在底面积为 $250c{m}^2$的圆柱形容器的底部，物体浸没在煤油中，如图所示， $\left(g=10N/\mathit{kg},{\rho }_{\mathit{煤油}}=0.8\times {10}^3\mathit{kg}/m^3\right)$

（1）细线受到的拉力是多大？

（2）若细线与物体脱落，待物体静止后煤油对容器底的压强变化了多少？