初中物理物质计算题

放在水平桌面上的薄壁圆柱形容器重4N，底面积100cm²，弹簧测力计的挂钩上挂着重为10N的物块，现将物块浸没水中，容器内水面由16cm上升到20cm(g=10N/kg)．

求：
（1）物块未放入水中时，容器底受到的水的压强；
（2）物块的密度；
（3）物块受到的浮力；
（4）物块浸没水中后，容器对桌面的压强.

如图甲所示，在容器底部固定一轻质弹簧，弹簧上端连有一边长为0.1m的正方体物块A，当容器中水的深度为20cm时，物块A有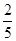的体积露出水面，此时弹簧恰好处于自然伸长状态（，g取）．求：

（1）物块A受到的浮力；
（2）物块A的密度；
（3）往容器缓慢加水（水未溢出）至物块A恰好浸没时水对容器底部压强的增加量△p（整个过程中弹簧受到的拉力跟弹簧的伸长量关系如图乙所示）．

下图是我国设计的北京2008年奥运会奖牌，奖牌正面为国际奥委会统一规定的图案，奖牌背面镶嵌着取自中国的玉石，形象诠释了中华民族自古以来以“玉”比“德”的价值观，是中华文明与奥林匹克精神的一次“中西合璧”。奖牌分为金牌、银牌和铜牌。其中金牌由纯银、玉石、纯金组成，金牌的总体积约为，镶嵌玉石的体积约为，纯金的质量约为6g。（已知：，，）。请问：

(1)一枚金牌约需要玉石多少克？
(2)一枚金牌除了玉石和纯金外，还需纯银约多少克？（计算结果保留一位小数）

小红的妈妈到某工艺品商店买了一件用金铜合金制成的实心工艺品，商店的售货员告诉她：这件工艺品是由质量相等的金、铜两种金属混合制成的，含金量为50％．小红的妈妈对商店售货员的话表示怀疑，让小红进行验证．小红通过实验测出工艺品的质量为600g，体积为52cm³，并从课本中查出了金、铜的密度分别是和8．9g/cm³．
（1）请根据小红的实验结果计算工艺品的密度．
（2）请根据售货员的说法，计算出工艺品的密度．并说明售货员的话是否可信．
（3）请计算这件工艺品的实际含金量．（最后两问结果保留小数点后面一位）

今年小明家种植柑橘获得了丰收。小明想：柑橘的密度是多少呢？于是，他将柑橘带到学校实验室，用天平、溢水杯来测量柑橘的密度。他用天平测出一个柑橘的质量是114 g，测得装满水的溢水杯的总质量是360 g；然后借助牙签使这个柑橘浸没在溢水杯中，当溢水杯停止排水后再取出柑橘，接着测得溢水杯的总质量是240 g。
请根据上述实验过程解答下列问题：
（1）溢水杯中排出水的质量是多大？
（2）这个柑橘的体积和密度各是多大？
（3）小明用这种方法测出的这个柑橘的密度与它的实际密度比较，是偏大还是偏小？为什么？

如图甲所示，在容器底部固定一轻质弹簧，弹簧上端连有一边长为0.1m的正方体物块A，当容器中水的深度为20cm时，物块A有的体积露出水面，此时弹簧恰好处于自然伸长状态（ρ_水=1.0×10³kg/m³，g取10N/kg）．求：

（1）物块A受到的浮力；
（2）物块A的密度；
（3）往容器缓慢加水（水未溢出）至物块A恰好浸没时水对容器底部压强的增加量△p（整个过程中弹簧受到的拉力跟弹簧的伸长量关系如图乙所示）．

有一个质量为0.232kg的铜铝合金球，其中含有0.054kg的铝。问合金球的密度是多少？（）

小明利用天平和量杯测量某种液体的密度，得到“液体体积V”和“液体与量筒的总质量m”的关系如下图所示，

求：
（1）量杯的质量是多大？
（2）该液体的密度是多大？
（3）通过上题表对照知该液体可能是什么？
（4）如果量杯中装入了体积为50mL的冰，当它熔化成水后体积为多少？

将一个容器内装满水后总质量为78g，再往此容器内装入20g沙石后总质量为90g。求：
（1）加入容器内的沙石的体积；（2）沙石的密度。

图的装置主要由长木板甲、物块乙和丙、定滑轮S和动滑轮P、水箱K、配重C和D及杠杆AB组成。C、D分别与支架固连在AB两端，支架与AB垂直，AB可绕支点O在竖直平面内转动。C通过细绳与P相连，绕在P上的绳子的一端通过固定在墙上的S连接到乙上，乙的另一端用绳子通过固定在桌面上的定滑轮与丙连接，乙置于甲上，甲放在光滑的水平桌面上。已知C重100N，D重10 N，丙重20N，OA:OB＝1:2，在物体运动的过程中，杠杆始终保持水平位置平衡。若在D上施加竖直向下F₀=20N的压力，同时在甲的左端施加水平向左的拉力F，甲恰好向左匀速直线运动，乙相对桌面恰好静止；若撤去拉力F改为在甲的右端施加水平向右的拉力F＇时，甲恰好在桌面上向右匀速直线运动，要继续保持乙相对桌面静止，则此时在D上施加竖直向下的压力为F₁；若移动K，将丙浸没水中，在拉力F＇作用下，甲仍向右匀速直线运动且乙相对桌面静止，则此时在D上施加竖直向下的压力为F₂。已知ρ_丙=2×10³kg/m³，F₁:F₂=4:5。杠杆、支架和不可伸缩细绳的质量、滑轮与轴的摩擦、杠杆与轴的摩擦均忽略不计。g取10N/kg。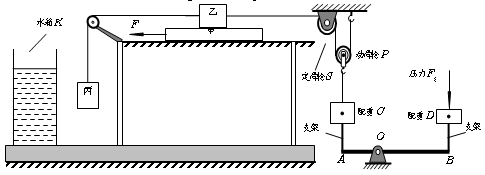

求：（1）丙浸没水中后受到的浮力F_浮；
（2）拉力F。

某提升装置中，杠杆AB能绕固定点O在竖直平面内转动，水平地面上的配重乙通过细绳竖直拉着杠杆B端。已知AO：OB=2：5，配重乙与地面的接触面积为S且S=200cm²。当在动滑轮下面挂上重1000N的物体甲静止时（甲未浸入水中），竖直向下拉绳子自由端的力为T₁，杠杆在水平位置平衡，此时配重乙对地面的压强为P₁且P₁=3.5×10⁴Pa；如果在动滑轮下挂一个质量为动滑轮质量5倍的物体丙，并把物体丙浸没在水中静止时，如图22甲所示，竖直向上拉绳子自由端的力为T₂，杠杆在水平位置平衡。此时配重乙对地面的压强为P₂且P₂=5.6×10⁴Pa。已知物体丙的质量与体积的关系的图像如图乙所示，如果不计杠杆重、绳重和滑轮轴间摩擦，图中两个滑轮所受重力相同取g=10N/kg。配重乙的体积为5×10^-2m³，求配重乙的密度。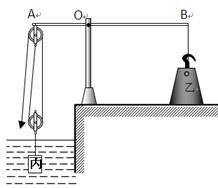

甲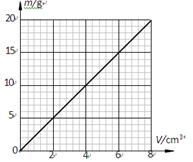

乙

如图甲所示，冰冻是造成高山地区冬季输配电线路倒塔（杆）断线的重要原因。为了避免这类事故的发生，一方面电力工人要及时对输电线路进行除冰作业，另一方面要加强输电线的抗拉能力。一般高压输电线每一根都是由一股位于中间的钢质线芯和六股相同粗细的铝质线芯绞在一起组成的，其横截面如图乙所示。这种输电线通常被称为钢芯铝绞线（代号LGJ）。已知该钢芯铝绞线所能承受的最大安全拉力为其正常工作情况下拉力的5倍。下表是该种钢芯铝绞线的相关技术数据。


1．该电力线路采用钢芯铝绞线而不采用与之同样结构尺寸的铝绞线，其主要目的是什么?
2．输电线路结冰后，输电线（连同上面的冰）变粗、变重。为了保证输电线路的安全，防止输电线被拉断，在冰冻的钢芯铝绞线（连同上面的冰，其横截面可以看作圆）的直径D增大到一定值时就必须进行除冰作业，试估算需要进行除冰作业时冰冻的钢芯铝绞线的直径D。（ρ_铝＝2.7×10³kg／m³，ρ_钢＝7.9×10³kg／m³，ρ_冰＝0.9×10³kg／m³，取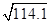＝10.7）
3．有一种输电线路除冰作业的方法叫“短路熔冰”。所谓“短路熔冰”，就是在短时间内，输电线不经过用电器而直接接通，输电线中通过比平时大许多的电流，利用导线本身发热熔冰以完成除冰作业的方法。短路熔冰时，若一根这种钢芯铝绞线每米的发热功率为200W，则短路熔冰时通过一根钢芯铝绞线的电流大约是多大?（取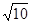＝3.2）