若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 的解是负整数,则所有满足条件的整数 的值之和是( )
| A. |
﹣26 |
B. |
﹣24 |
C. |
﹣15 |
D. |
﹣13 |
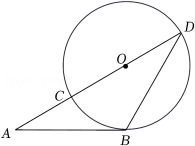
如图,AB是 的切线,B为切点,连接AO交 于点C,延长AO交 于点D,连接BD.若 ,且 ,则AB的长度是( )
| A. |
3 |
B. |
4 |
C. |
|
D. |
|
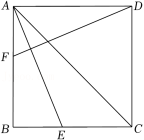
如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若 ,则∠CDF的度数为( )
| A. |
45° |
B. |
60° |
C. |
67.5° |
D. |
77.5° |
小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为 ,根据题意,下面所列方程正确的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
估计 )的值应在( )
| A. |
10和11之间 |
B. |
9和10之间 |
C. |
8和9之间 |
D. |
7和8之间 |
用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为( )

| A. |
32 |
B. |
34 |
C. |
37 |
D. |
41 |
如图,△ABC与△DEF位似,点O为位似中心,相似比为 .若△ABC的周长为4,则△DEF的周长是( )

| A. |
4 |
B. |
6 |
C. |
9 |
D. |
16 |
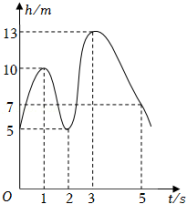
如图,曲线表示一只蝴蝶在飞行过程中离地面的高度h(m)随飞行时间t(s)的变化情况,则这只蝴蝶飞行的最高高度约为( )
| A. |
5m |
B. |
7m |
C. |
10m |
D. |
13m |
如图,直线AB,CD被直线CE所截, , ,则 的度数为( )

| A. |
40° |
B. |
50° |
C. |
130° |
D. |
150° |
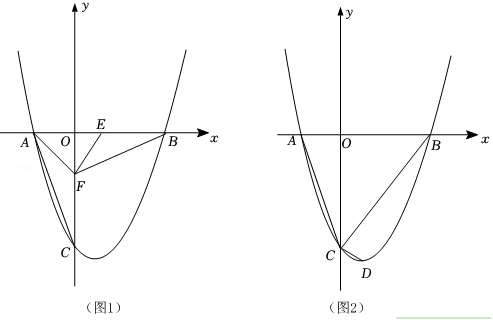
在平面直角坐标系中,抛物线 与 轴相交于点 (点 在点 的左侧),与 轴相交于点 ,连接 .
(1)求点 ,点 的坐标;
(2)如图1,点 在线段 上(点 不与点 重合),点 在 轴负半轴上, ,连接 ,设 的面积为 , 的面积为 , ,当 取最大值时,求 的值;
(3)如图2,抛物线的顶点为 ,连接 ,点 在第一象限的抛物线上, 与 相交于点 ,是否存在点 ,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.
综合与实践
问题情境:数学活动课上,王老师出示了一个问题:
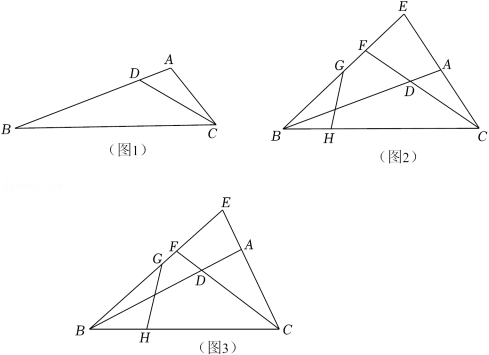
如图1,在 中, 是 上一点, .求证 .
独立思考:(1)请解答王老师提出的问题.
实践探究:(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
“如图2,延长 至点 ,使 , 与 的延长线相交于点 ,点 分别在 上, .在图中找出与 相等的线段,并证明.”
问题解决:(3)数学活动小组同学对上述问题进行特殊化研究之后发现,当 时,若给出 中任意两边长,则图3中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.
“如图3,在(2)的条件下,若 ,求 的长.”
如图,在 中, , ,点 在 上, ,连接 , ,点 是边 上一动点(点 不与点 重合),过点 作 的垂线,与 相交于点 ,连接 ,设 , 与 重叠部分的面积为 .
(1)求 的长;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.
