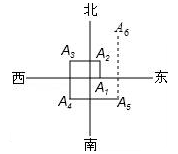
如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是 m.
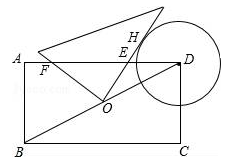
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 .
如图,直线y=x-2与x轴、y轴分别交于M、N两点,现有半径为1的动圆圆心位于原点处,并以每秒1个单位的速度向右作平移运动.已知动圆在移动过程中与直线MN有公共点产生,当第一次出现公共点到最后一次出现公共点,这样一次过程中该动圆一共移动 秒.

在反比例函数 的图象上,有一系列点
的图象上,有一系列点 ,若
,若 的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点
的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点 ,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为
,作x轴与y轴的垂线段,构成若干个矩形如下图所示,将图中阴影部分的面积从左到右依次记为 ,则
,则 ______.(用n的代数式表示)
______.(用n的代数式表示)
设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是_______.(填写所有正确结论的序号)①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是0;④存在实数x,使[x)-x=0.5成立。
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形 ;再顺次连结菱形
;再顺次连结菱形 的各边中点,得矩形
的各边中点,得矩形 ;再顺次连结矩形
;再顺次连结矩形 的各边中点,得菱形
的各边中点,得菱形 ,……这样继续下去.则图中的四边形
,……这样继续下去.则图中的四边形 的周长等于 ,图中的四边形
的周长等于 ,图中的四边形 的面积等于 .
的面积等于 .

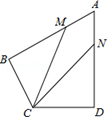
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
规定一种新的运算:对于一个合数n,(n)表示不是n的素因数的最小素数,如(4)=3,(12)
=5.那么(60)+(84)的值是 .
如图,在扇形AOB中,∠AOB=90°,弧AB的长为2π,则扇形AOB的面积为 .
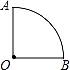
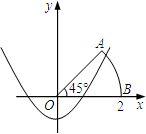
如图,以扇形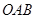 的顶点
的顶点 为原点,半径
为原点,半径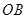 所在的直线为
所在的直线为 轴,建立平面直角坐标系,点
轴,建立平面直角坐标系,点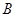 的坐标为
的坐标为 ,若抛物线
,若抛物线 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数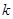 的取值范围是 .
的取值范围是 .
阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,使它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是 ,由题意得方程组:
,由题意得方程组: ,
,
消去y化简得: ,
,
∵△=49-48=1>0,∴x1= ,x2= .
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?