初中数学四种命题及其关系试题

函数y＝x和在同一直角坐标系中的图象大致是（   ）

重庆一中初三学生小欣暑假骑车沿直线旅行，先前进了1000米，休息了一段时间，又原路返回500米，再前进了1000米，则她离起点的距离与时间的关系示意图是
 

（本小题满分8分）星期天，小明与小刚骑自行车去距家

50千米的某地旅游，匀速行驶1.5小时的时候，其中一
辆自行车出故障，因此二人在自行车修理点修车，用了
半个小时，然后以原速继续前行，行驶1小时到达目的
地．请在右面的平面直角坐标系中，画出符合他们行驶
的路程S（千米）与行驶时间t（时）之间的函数图象．

已知，一次函数y＝kx＋b的图像与正比例函数y＝x交于点A，并与y轴交于点B(0，－4)，△AOB的面积为6，则kb＝         。

．父亲节，学校“文苑”专栏登出了某同学回忆父亲的小诗：“同辞家门赴车站，别时叮咛语千万，学子满载信心去，老父怀抱希望还。”如果用纵轴表示父亲和学子在行进中离家的距离，横轴t表示离家的时间，那么下面与上述诗意大致相吻的图象是

 

﹣如图，火车匀速通过隧道（隧道长大于火车长）时，火车进入隧道的时间与火车在隧道内的长度之间的关系用图象描述大致是(     )　

 
Ａ．                  B．               C．              D．

函数y＝x和在同一直角坐标系中的图象大致是

矩形面积为4，长是宽的函数，其函数图像大致是（  ）

某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：

年   度	2001	2002	2003	2004
投入技改资金z(万元)	2.5	3	4	4.5
产品成本，(万元／件)	7.2	6	4.5	4

(1)请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
(2)按照这种变化规律，若2005年已投人技改资金5万元．
①预计生产成本每件比2004年降低多少万元?
②如果打算在2005年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元（结果精确到0.01万元)?

（本小题满分12分）如图，已知一次函数y＝kx＋b的图象交反比例函数
的图象于点A、B，交x轴于点C．
(1)求m的取值范围；
(2)若点A的坐标是(2，－4)，且＝，求m的值和一次函数的解析式．

如图3，在矩形ABCD中，AB＝4，BC＝3，点F在DC边上运动，连结AF，过
点B作BE⊥AF于E，设BE＝y，AF＝x，则能反映y与x之间函数关系的大致图象是（   ）
A                B               C                D

A、B两地相距360km，甲车以100km/h的速度从A地驶往B地，乙车以80km/h
的速度从B地驶往A地，两车同时出发．设乙车行驶的时间为x(h),两车之间的距离为y(km)，
则y与x之间的函数关系的图象是（   ▲  ）

如图，矩形中，，，是的中点，点在矩形的边上沿运动，则的面积与点经过的路程之间的函数关系用图象表示大致是下图中的
       
C                      D

一电工沿着如图所示的梯子NL往上爬，当他爬到中点M处时，由于地面太滑，梯
子沿墙面与地面滑下，设点M的坐标为（x，y）（x>0）,则y与x之间的函数关系用图象表
示大致是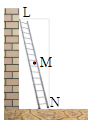   
     

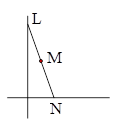
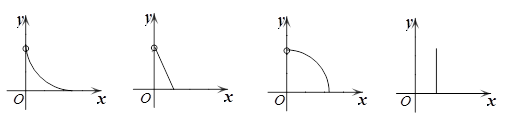
A．                B．             C．              D．

如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°， AB=6，AD=9，
点E是CD上的一个动点(E不与D重合)，过点E作EF∥AC，交AD于点F(当E运
动到C时，EF与AC重合巫台)．把△DEF沿EF对折，点D的对应点是点G，设DE=x，
△GEF与梯形ABCD重叠部分的面积为y。
(1) 求CD的长及∠1的度数；
(2) 若点G恰好在BC上，求此时x的值；
(3) 求y与x之间的函数关系式。并求x为何值时，y的值最大?最大值是多少?