[湖南]2011年湖南省长沙市九年级毕业学业考试模拟试卷(四)数学卷
根据下表中的二次函数 的自变量
的自变量 与函数
与函数 的对应值,可判断该二次函数的图象与
的对应值,可判断该二次函数的图象与 轴( ).
轴( ).
| A.只有一个交点 | B.有两个交点,且它们分别在 轴两侧 轴两侧 |
C.有两个交点,且它们均在 轴同侧 轴同侧 |
D.无交点 |
下列命题是假命题的是( )
A.若 ,则x+2008<y+2008 ,则x+2008<y+2008 |
B.单项式 的系数是-4 的系数是-4 |
C.若 则 则 |
D.平移不改变图形的形状和大小 |
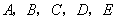 五个景点之间的路线如图所示.若每条路线的里程
五个景点之间的路线如图所示.若每条路线的里程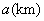 及行驶的平均速度
及行驶的平均速度 用
用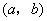 表示,则从景点
表示,则从景点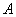 到景点
到景点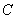 用时最少的路线是( )
用时最少的路线是( )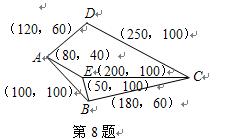
A.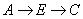 |
B.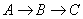 |
C.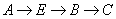 |
D.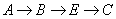 |
已知某函数的图象经过点A (1 , 2) ,且函数 的值随自变量
的值随自变量 的值的增大而减小, 请你写出一个符合条件的函数表达式 .
的值的增大而减小, 请你写出一个符合条件的函数表达式 .
如图,⊙O的半径为12cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以2 的速度沿圆周逆时针运动,当点P回到点A就停止运动.当点P运动的时间为 s时,BP与⊙O相切.
的速度沿圆周逆时针运动,当点P回到点A就停止运动.当点P运动的时间为 s时,BP与⊙O相切.
建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点E离D多远,正好使A、C、E成一直线.
某单位欲招聘一名员工,现有 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
(1). 请将表一和图一中的空缺部分补充完整;
(2). 竞聘的最后一个程序是由该单位的 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
(3). 若每票计 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按 的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图
(1). 若 ,则
,则

(2). 若 ,那么
,那么 吗?说明你的理由。
吗?说明你的理由。
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2008年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元.
(1). 求A市投资“改水工程”的年平均增长率;
(2). 从2008年到2010年,A市三年共投资“改水工程”多少万元?600+600×1.4+1176=2616(万元).A市三年共投资
如图,方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.求:
(1). cos∠F的值;
(2). BE的长.
建设新农村,农村大变样.向阳村建起了天然气供应站,气站根据实际情况,每天从零点开始至凌晨4点,只打开进气阀,在以后的16小时(4∶00-20∶00),同时打开进气阀和供气阀,20∶00-24∶00只打开供气阀,已知气站每小时进气量和供气量是一定的,下图反映了某天储气量 与
与 (小时)之间的关系.
(小时)之间的关系.
(1). 求0∶00-20∶00之间气站每小时增加的储气量;
(2). 求20∶00-24∶00时, 与
与 的函数关系式,并画出函数图象;
的函数关系式,并画出函数图象;
(3). 照此规律运行,从这天零点起三昼夜内,经过__小时气站储气量达到最大?最大值为___ .(请把答案直接写在在横线上,不必写过程)
.(请把答案直接写在在横线上,不必写过程)
 的3倍与
的3倍与 的平方的差”,正确的是( )
的平方的差”,正确的是( )



 ,若
,若 ,则
,则 的值是( )
的值是( )
 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( ) 




 的值为0,则x的值为 .
的值为0,则x的值为 .


 ,….试猜想第
,….试猜想第 个等式(
个等式( .
.
 ,
, ,求代数式
,求代数式 的值。
的值。 ;并写出它的整数解。
;并写出它的整数解。 与x轴交于A(1,0)、B(5,0)两点.
与x轴交于A(1,0)、B(5,0)两点.
 (0°<
(0°< ,求s与t之间的函数关系式.
,求s与t之间的函数关系式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号